
分析 建立如图所示的坐标系,在x轴上取点B(-$\sqrt{3}$,0),D($\sqrt{3}$,0),在y轴上取点A(0,$\frac{1}{2}$),C(0,-$\frac{1}{2}$),即可求出直视图的面积.
解答  解:建立如图所示的坐标系,在x轴上取点B(-$\sqrt{3}$,0),D($\sqrt{3}$,0),
解:建立如图所示的坐标系,在x轴上取点B(-$\sqrt{3}$,0),D($\sqrt{3}$,0),
在y轴上取点A(0,$\frac{1}{2}$),C(0,-$\frac{1}{2}$),依次连接AB,BC,DA,则四边形ABCD为所求,
∴一角为60°,边长是2cm 的菱形的直观图的面积是2×$\frac{1}{2}$×2$\sqrt{3}$×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$cm2.
点评 本题考查斜二测法画直观图,考查学生的作图能力,比较基础.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 综合得分k的范围 | 产品级别 | 产品利润率 |
| k≥85 | 一级 | a |
| 75≤k<85 | 二级 | 5a2 |
| 70≤k<75 | 三级 | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
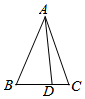 如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.
如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 120 | C. | 240 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com