
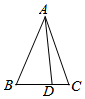 如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.
如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3. 分析 根据三角形边角之间的关系,结合正弦定理和余弦定理即可得到结论.
解答 解:在△ABC中,∵cos∠ADC=$\frac{1}{7}$,
∴sin∠ADC=$\sqrt{1-\frac{1}{49}}$=$\frac{4\sqrt{3}}{7}$,
则sin∠BAD=sin(∠ADC-∠B)=sin∠ADC•cosB-cos∠ADC•sinB=$\frac{4\sqrt{3}}{7}$×$\frac{1}{2}$-$\frac{1}{7}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{14}$.
在△ABD中,由正弦定理得BD=$\frac{AB•sin∠BAD}{sin∠ADB}$=$\frac{8×\frac{3\sqrt{3}}{14}}{\frac{4\sqrt{3}}{7}}$=3.
故答案为:$\frac{{3\sqrt{3}}}{14},3$.
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理是解决本题本题的关键,难度不大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 105 | B. | 507 | C. | 071 | D. | 717 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com