
分析 (1)根据向量共线的等价条件建立方程关系进行求解判断,
(2)根据向量垂直的等价条件进行判断,
(3)根据向量数量积的应用求向量夹角即可.
解答 解:∵$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的单位向量,
∴$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=|$\overrightarrow{{e}_{1}}$||$\overrightarrow{{e}_{2}}$|cos$\frac{π}{3}$=1×1×$\frac{1}{2}$=$\frac{1}{2}$.
(1)若向量$\overrightarrow{c}$=k$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$,
若$\overrightarrow{c}$与$\overrightarrow{b}$共线,
则$\overrightarrow{c}$=m$\overrightarrow{b}$,即k$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$=m(-3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$),
则$\left\{\begin{array}{l}{k=-3m}\\{-2=2m}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-1}\\{k=3}\end{array}\right.$,即当k=3时,$\overrightarrow{c}$与$\overrightarrow{b}$能共线,当k≠3是,$\overrightarrow{c}$与$\overrightarrow{b}$不能共线.
(2)若$\overrightarrow{c}$=k$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$且$\overrightarrow{c}$与$\overrightarrow{a}$垂直,
则$\overrightarrow{c}$•$\overrightarrow{a}$=(k$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$)•(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)=0,
即2k$\overrightarrow{{e}_{1}}$2-2$\overrightarrow{{e}_{2}}$2+(k-4)$\overrightarrow{{e}_{1}}$′$\overrightarrow{{e}_{2}}$=0
即2k-2+(k-4)×$\frac{1}{2}$=0.
得k=$\frac{8}{5}$;
(3)|$\overrightarrow{a}$|2=4$\overrightarrow{{e}_{1}}$2+$\overrightarrow{{e}_{2}}$2+4$\overrightarrow{{e}_{1}}$′$\overrightarrow{{e}_{2}}$=4+1+4×$\frac{1}{2}$=7,
|$\overrightarrow{b}$|2=9$\overrightarrow{{e}_{1}}$2+4$\overrightarrow{{e}_{2}}$2-12$\overrightarrow{{e}_{1}}$′$\overrightarrow{{e}_{2}}$=9+4-12×$\frac{1}{2}$=7,
即|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{7}$,
$\overrightarrow{a}$•$\overrightarrow{b}$=(2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$)•(-3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$)=-6$\overrightarrow{{e}_{1}}$2+4$\overrightarrow{{e}_{2}}$2+$\overrightarrow{{e}_{1}}$′$\overrightarrow{{e}_{2}}$=-6+4-$\frac{1}{2}$=$-\frac{5}{2}$,
则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-\frac{5}{2}}{\sqrt{7}×\sqrt{7}}$=-$\frac{5}{14}$.
点评 本题主要考查向量共线,向量垂直以及向量数量积的应用,综合性考查向量的性质和应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
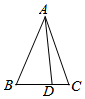 如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.
如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 120 | C. | 240 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com