
分析 (Ⅰ)利用利润=盈利-亏损,得到y与p的关系,将p代入整理即可;
(Ⅱ)对(Ⅰ)的解析式求导,判定取最大值时的x值,求最大利润.
解答 解:(I)由题意,所获得的利润为
y=10[2(x-p)-p]=10(2x-3p)=20x-30p=20x-3x2+96lnx-90(4≤x≤12)
(II)由(Ⅰ)得y'=20-6x+$\frac{96}{x}$=$\frac{-6{x}^{2}+20x+96}{x}=\frac{-2(3x+8)(x-6)}{x}$,
令y'=0,得到x=6或x=-$\frac{8}{3}$(舍去);
所以当4≤x<6,y'>0,函数在[4,6]为增函数,当6<x<12时,y'<0,函数在(6,12)为减函数;
所以当x=6时,函数去极大值,即最大值,
所以当x=6时利润最大,为20×6-3×62+96ln6-90=96ln6-78(万元),
当每台机器的日产量为6(万件)时所获得的利润最大,最大利润为96ln6-78万元.
点评 本题考查了导数的实际应用,关键是建立函数关系,利用求导,求最值.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
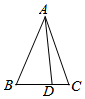 如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.
如图,在△ABC中,∠B=$\frac{π}{3}$,AB=8,点D在边BC上,cos∠ADC=$\frac{1}{7}$,则sin∠BAD=$\frac{3\sqrt{3}}{14}$,BD=3.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 200 | B. | 120 | C. | 240 | D. | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形或直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{4}$ | C. | $\frac{{\sqrt{2}+\sqrt{3}}}{4}$ | D. | $\sqrt{\frac{{\sqrt{5}-1}}{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com