练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．如图，在半径为R的圆内随机撒一粒黄豆，它落在阴影部分内接正三角形上的概率是$\frac{3\sqrt{3}}{4π}$

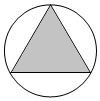
    分析 根据几何概型的概率公式，分别求出正三角形和圆的面积，代入几何概型公式，即可得到答案．

    解答 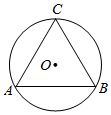解：设圆O是半径为R=2，圆O的面积为πR2=4π
    则圆内接正三角形的边长为2$\sqrt{3}$，而正三角形ABC的面积为$\frac{\sqrt{3}}{4}×（2\sqrt{3}）^{2}$=3$\sqrt{3}$，
    ∴豆子落在正三角形ABC内的概率P=$\frac{3\sqrt{3}}{4π}$．
    故答案为：$\frac{3\sqrt{3}}{4π}$．

    点评 本题主要考查几何概型中的面积类型，基本方法是：分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积，两者求比值，即为概率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知曲线C1：$\left\{{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}}$（θ为参数），曲线C2：$\left\{{\begin{array}{l}{x=\frac{{\sqrt{2}}}{2}t-\sqrt{2}}\\{y=\frac{{\sqrt{2}}}{2}t}\end{array}}$（t为参数）．
    （1）指出C1，C2各是什么曲线；
    （2）求曲线C1与C2公共点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．一个四面体，其中一个顶点A的三个角分别为60°，θ，90°，其中tanθ=2，则θ角与60°角所在面的二面角的余弦值为$-\frac{{\sqrt{3}}}{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．圆心在抛物线x2=2y上且与直线2x+2y-3=0相切的圆中，面积最小的圆的方程为$（x+1）^{2}+（y-\frac{1}{2}）^{2}$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．为了响应政府“节能、降耗、减排、增效”的号召，某工厂决定转产节能灯，现有A、B两种型号节能灯的生产线．在这两种生产线的大量产品中各随机抽取100个进行质量评估，经检测，综合得分情况如图的频率分布直方图：

    产品级别划分以及利润率如表，其中$\frac{1}{10}$＜a＜$\frac{1}{6}$；将频率视为概率．
    综合得分k的范围产品级别产品利润率
    k≥85一级a
    75≤k＜85二级5a2
    70≤k＜75三级a2
    （Ⅰ）在A型节能灯中按产品级别用分层抽样的方法抽取10个，在这10个节能灯中随机抽取3个，至少有2个一级品的概率是多少？
    （Ⅱ）从长期来看，投资哪种型号的节能灯的平均利润率较大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知复数z=$\frac{2}{1-i}$-2i，则z的共轭复数是（　　）
    A．1-iB．1+2iC．1-2iD．1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设函数f（x）是定义在（-∞，0）上的可导函数，其导函数为f'（x），且3f（x）+xf'（x）＜0，则不等式（x+2016）3f（x+2016）+8f（-2）＜0的解集是（-2018，-2016）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

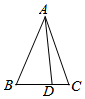    18．如图，在△ABC中，∠B=$\frac{π}{3}$，AB=8，点D在边BC上，cos∠ADC=$\frac{1}{7}$，则sin∠BAD=$\frac{3\sqrt{3}}{14}$，BD=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在△ABC中，a、b、c分别是角A、B、C的对边，已知a2cosAsinB=b2sinAcosB，则△ABC为（　　）
    A．等腰三角形B．等腰直角三角形
    C．直角三角形D．等腰三角形或直角三角形

    查看答案和解析>>

    同步练习册答案