
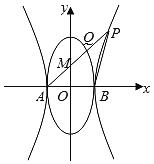
【题目】如图,椭圆![]() 的左、右顶点分别为A、B,双曲线
的左、右顶点分别为A、B,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,点P是
,点P是![]() 上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为
上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为![]()
![]() 为坐标原点.
为坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)求点M的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() 使得直线BP与直线OM关于直线
使得直线BP与直线OM关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为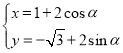 (其中
(其中![]() 为参数,
为参数,![]() ).在极坐标系(以坐标原点
).在极坐标系(以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 上恰有一个点到曲线
上恰有一个点到曲线![]() 的距离为1,求曲线
的距离为1,求曲线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线l不经过坐标原点O且不平行与坐标轴,l与
,直线l不经过坐标原点O且不平行与坐标轴,l与![]() 相交于A,B两点,线段
相交于A,B两点,线段![]() 的中点为M.
的中点为M.
(1)证明:直线![]() 的斜率与直线l的斜率的乘积为定值;
的斜率与直线l的斜率的乘积为定值;
(2)若直线l过点![]() ,延长线
,延长线![]() 与
与![]() 交于点P,若四边形
交于点P,若四边形![]() 是平行四边形,求直线l的斜率;
是平行四边形,求直线l的斜率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从2开始的连续偶数蛇形排列形成宝塔形数表,第一行为2,第一行为46,第三行为12,10,8,第四行为14,16,18,20.如图所示,在宝塔形数表中位于第i行,第j列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,,若
,,若![]() ,则
,则![]() ( )
( )
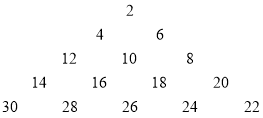
A.65B.70C.71D.72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com