
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)对函数![]() 求导,求
求导,求![]() ,
,![]() ,然后利用点斜式方程可求得答案;
,然后利用点斜式方程可求得答案;
(2)对函数![]() 求导,构造函数
求导,构造函数![]() 判断其在
判断其在![]() 上单调递增,分类讨论
上单调递增,分类讨论![]() 时:判断函数
时:判断函数![]() 单调递增函数,然后再由
单调递增函数,然后再由![]() 求得
求得![]() 的取值范围;
的取值范围;![]() 时,
时,![]() 使得
使得![]() ,判断在
,判断在![]() 上函数
上函数![]() 单调递减,
单调递减,![]() 上单调递增,求得函数最小值
上单调递增,求得函数最小值![]() 然后利用
然后利用![]() 和
和![]() 进行适当地转化即可求出参数
进行适当地转化即可求出参数![]() 的取值范围,最后总结讨论结果得出
的取值范围,最后总结讨论结果得出![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,
则![]() ,
,![]() ,由点斜式方程可得:
,由点斜式方程可得:![]() 化简得:
化简得:![]() ,
,
即切线方程为![]() .
.
(2)由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() .
.
所以![]() 在
在![]() 上单调递增,且
上单调递增,且![]() .
.
①当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,
单调递增,
由于![]() 恒成立,则有
恒成立,则有![]() ,即
,即![]() ,
,
所以![]() 满足条件;
满足条件;
②当![]() 时,则存在
时,则存在![]() ,使得
,使得![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,则
,则![]() ,
,![]() 单调递增.
单调递增.
所以![]() ,
,
又![]() 满足
满足![]() ,即
,即![]() ,
,
所以![]() ,则
,则![]() ,即
,即![]() ,得
,得![]() .
.
又![]() ,令
,令![]() ,则
,则![]() ,
,
可知,当![]() 时,
时,![]() ,则
,则![]() 单调递减,
单调递减,
所以![]() ,
,
此时![]() 满足条件.
满足条件.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
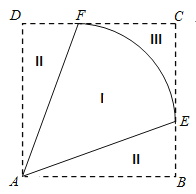
【题目】某地拟规划种植一批芍药,为了美观,将种植区域(区域I)设计成半径为1km的扇形![]() ,中心角
,中心角![]() (
(![]() ).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形
).为方便观赏,增加收入,在种植区域外围规划观赏区(区域II)和休闲区(区域III),并将外围区域按如图所示的方案扩建成正方形![]() ,其中点
,其中点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
上.已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.
(1)要使观赏区的年收入不低于5万元,求![]() 的最大值;
的最大值;
(2)试问:当![]() 为多少时,年总收入最大?
为多少时,年总收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
科目:高中数学 来源: 题型:
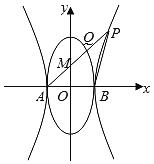
【题目】如图,椭圆![]() 的左、右顶点分别为A、B,双曲线
的左、右顶点分别为A、B,双曲线![]() 以A、B为顶点,焦距为
以A、B为顶点,焦距为![]() ,点P是
,点P是![]() 上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为
上在第一象限内的动点,直线AP与椭圆相交于另一点Q,线段AQ的中点为M,记直线AP的斜率为![]()
![]() 为坐标原点.
为坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)求点M的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() 使得直线BP与直线OM关于直线
使得直线BP与直线OM关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将初始温度为![]() 的物体放在室温恒定为
的物体放在室温恒定为![]() 的实验室里,现等时间间隔测量物体温度,将第
的实验室里,现等时间间隔测量物体温度,将第![]() 次测量得到的物体温度记为
次测量得到的物体温度记为![]() ,已知
,已知![]() .已知物体温度的变化与实验室和物体温度差成正比(比例系数为
.已知物体温度的变化与实验室和物体温度差成正比(比例系数为![]() ).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
在上述模型下,设物体温度从![]() 升到
升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,那么
,那么![]() 与
与![]() 的大小关系是________(用“
的大小关系是________(用“![]() ”,“
”,“![]() ”或“
”或“![]() ”号填空)
”号填空)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上的两点,点
上的两点,点![]() 的纵坐标分别为1,2,分别过点
的纵坐标分别为1,2,分别过点![]() 作倾斜角互补的两条直线交抛物线
作倾斜角互补的两条直线交抛物线![]() 于另外不同两点
于另外不同两点![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有![]() 行数表如下:
行数表如下:
第一行:![]()
第二行:![]()
第三行:![]()
…… …… ……
第![]() 行:
行:![]()
第m行:![]()
按照上述方式从第一行写到第m行(写下的第n个数记作![]() )得到有穷数列
)得到有穷数列![]() ,其前n项和为
,其前n项和为![]() ,若
,若![]() 存在,则
存在,则![]() 的最小值为______
的最小值为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com