
【题目】已知函数![]() .
.
(1)求函数![]() 的值域;
的值域;
(2)在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)请叙述余弦定理(写出其中一个式子即可)并加以证明.
【答案】(1)![]() ;(2)2;(3)详见解析
;(2)2;(3)详见解析
【解析】
(1)推导出f(x)![]() cosx=2sin(x
cosx=2sin(x![]() ),由此能求出函数f(x)的值域.
),由此能求出函数f(x)的值域.
(2)由f(B)=2,得到f(B)=2sin(B![]() )=2,B∈(0,π),求出B
)=2,B∈(0,π),求出B![]() ,由余弦定理得:3=a2+c2﹣2accos
,由余弦定理得:3=a2+c2﹣2accos![]() ,由△ABC面积S得ac=1,由此能求出a+c.
,由△ABC面积S得ac=1,由此能求出a+c.
(3)建立坐标系,用解析法即可证明余弦定理.
(1)∵![]() .
.
∴f(x)![]() sinx﹣cosx=2sin(x
sinx﹣cosx=2sin(x![]() ),
),
∴由x∈R,可得:f(x)=2sin(x![]() )∈[﹣2,2];
)∈[﹣2,2];
(2)∵△ABC中,角A,B,C的对边分别为a,b,c,f(B)=2,
∴f(B)=2sin(B![]() )=2,B∈(0,π),
)=2,B∈(0,π),
∴B![]() ,
,
∵b![]() ,∴由余弦定理得:3=a2+c2﹣2accos
,∴由余弦定理得:3=a2+c2﹣2accos![]() ,
,
∵△ABC面积S![]() ,∴
,∴![]() acsinB
acsinB![]() ac
ac![]() ,解得ac=1,
,解得ac=1,
∴a2+c2=3+2accos![]() 3﹣ac=2,
3﹣ac=2,
∴(a+c)2=a2+c2+2ac=2+2=4,
∴a+c=2.
(3)证明:余弦定理为:a2=b2+c2﹣2bccosA.
下用解析法证明:以A为原点,射线AB为x轴正向,建立直角坐标系,则得A(0,0),B(c,0),C(bcosA,bsinA).
由两点距离公式得:
a2=|BC|2=(c﹣bcosA)2+(﹣bsinA)2=b2+c2﹣2bccosA.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为线段
为线段![]() 上的动点(不含
上的动点(不含![]() ).
).
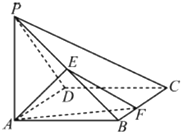
(1)平面![]() 与平面
与平面![]() 是否互相垂直?如果是,请证明;如果不是,请说明理由;
是否互相垂直?如果是,请证明;如果不是,请说明理由;
(2)求二面角![]() 的余弦值的取值范围.
的余弦值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一,此后由郑州市城市管理局起草公开征求意见,经专家论证,多次组织修改完善,数易其稿,最终形成《郑州市城市生活垃圾分类管理办法》(以下简称《办法》).《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过,并于2019年12月1日开始施行.《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类.为了获悉高中学生对垃圾分类的了解情况,某中学设计了一份调查问卷,500名学生参加测试,从中随机抽取了100名学生问卷,记录他们的分数,将数据分成7组:![]() ,
,![]() ,…,
,…,![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
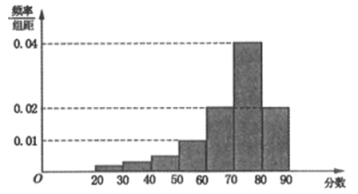
(1)从总体的500名学生中随机抽取一人,估计其分数不低于60的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间![]() 内的学生人数,
内的学生人数,
(3)学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类,我在实践”活动,以增强学生的环保意识.首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加,已知样本中分数小于40的5名学生中,男生3人,女生2人,求抽取的2人中男女同学各1人的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的4月23日为“世界读书日”,某调查机构对某校学生做了一个是否喜爱阅读的抽样调查.该调查机构从该校随机抽查了100名不同性别的学生(其中男生45名),统计了每个学生一个月的阅读时间,其阅读时间![]() (小时)的频率分布直方图如图所示:
(小时)的频率分布直方图如图所示:
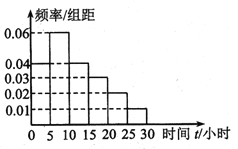
(1)求样本学生一个月阅读时间![]() 的中位数
的中位数![]() .
.
(2)已知样本中阅读时间低于![]() 的女生有30名,请根据题目信息完成下面的
的女生有30名,请根据题目信息完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
![]() 列联表
列联表
男 | 女 | 总计 | |
| |||
| |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
其中: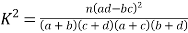 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}(an∈Z)的前n项和为Sn,记S1,S2,…,Sn中奇数的个数为bn.
(1)若an=n,请写出数列{bn}的前5项;
(2)求证:“a1为奇数,ai(i=2,3,4,…)为偶数”是“数列{bn}是单调递增数列”的充分不必要条件;
(3)若ai=bi,i=1,2,3,…,求数列{an}的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com