
【题目】已知函数![]() .
.
(1)讨论![]() 的导数
的导数![]() 的单调性;
的单调性;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,求实数
,求实数![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
【答案】(1)![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增;
上单调递增;
(2)见解析.
【解析】
(1)求出![]() ,令
,令![]() ,对
,对![]() ,
,![]() 讨论来求
讨论来求![]() 的单调性;
的单调性;
(2)将![]() 有两个极值点
有两个极值点![]() ,
,![]() 转化为
转化为![]() 有两解,继续转化为
有两解,继续转化为![]() 有两解,构造函数
有两解,构造函数![]() ,求导
,求导![]() 为其极小值,可得
为其极小值,可得![]() ,即可求得实数
,即可求得实数![]() 的取值范围;另外要证明
的取值范围;另外要证明![]() ,不妨设
,不妨设![]() ,则
,则![]() ,由(1)根据
,由(1)根据![]() 的单调性得
的单调性得![]() ,通过变形,转化为证明
,通过变形,转化为证明![]() ,进一步变形证明
,进一步变形证明![]() ,构造函数
,构造函数![]() ,利用导数研究其最小值即可证明.
,利用导数研究其最小值即可证明.
(1)由题意,得![]() .
.
设![]() ,则
,则![]() .
.
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
②当![]() 时,由
时,由![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增.
上单调递增.
(2)由于![]() 有两个极值点
有两个极值点![]() ,
,![]() ,即
,即![]() 在
在![]() 上有两解
上有两解![]() ,
,![]() ,
,
![]() 即
即![]() ,显然
,显然![]() ,故等价于
,故等价于![]() 有两解
有两解![]() ,
,![]() ,
,
设![]() ,则
,则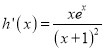 ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,
单调递减,
且![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递减,且
单调递减,且![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 单调递增,且
单调递增,且![]() 时,
时,![]() ,
,
所以![]() 是
是![]() 的极小值,
的极小值,![]() 有两解
有两解![]() ,
,![]() 等价于
等价于![]() ,得
,得![]() .
.
不妨设![]() ,则
,则![]() .
.
据(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,
,
由于![]() ,
,![]() ,且
,且![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
欲证明:![]() ,等价于证明:
,等价于证明:![]() ,
,
即证明:![]() ,只要证明:
,只要证明:![]() ,
,
因为![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以只要证明:![]() ,
,
由于![]() ,所以只要证明:
,所以只要证明:![]() ,
,
即证明:![]() ,
,
设![]() ,据(1)
,据(1)![]() ,
,
![]()
![]()
![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,
,
即![]() ,
,
故![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
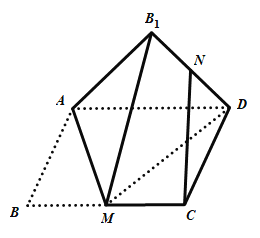
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“移动支付、高铁、网购、共享单车”被称为中国的“新四大发明”.为了帮助50岁以上的中老年人更快地适应“移动支付”,某机构通过网络组织50岁以上的中老年人学习移动支付相关知识.学习结束后,每人都进行限时答卷,得分都在![]() 内.在这些答卷(有大量答卷)中,随机抽出
内.在这些答卷(有大量答卷)中,随机抽出![]() 份,统计得分绘出频率分布直方图如图.
份,统计得分绘出频率分布直方图如图.
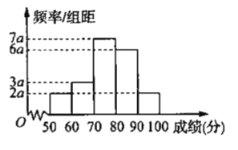
(1)求出图中![]() 的值,并求样本中,答卷成绩在
的值,并求样本中,答卷成绩在![]() 上的人数;
上的人数;
(2)以样本的频率为概率,从参加这次答卷的人群中,随机抽取![]() 名,记成绩在
名,记成绩在![]() 分以上(含
分以上(含![]() 分)的人数为
分)的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数.
的积函数.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰好为
的值域恰好为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,点O为对角线BD的中点,点E,F分别为棱PC,PD的中点,已知PA⊥AB,PA⊥AD.
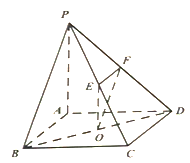
(1)求证:直线PB∥平面OEF;
(2)求证:平面OEF⊥平面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次数学考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班样本成绩的茎叶图如图所示.
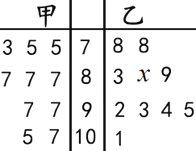
(1)用样本估计总体,若根据茎叶图计算得甲乙两个班级的平均分相同,求![]() 的值;
的值;
(2)从样本中任意抽取3名学生的成绩,若至少有两名学生的成绩相同的概率大于![]() ,则该班成绩判断为可疑.试判断甲班的成绩是否可疑?并说明理由.
,则该班成绩判断为可疑.试判断甲班的成绩是否可疑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,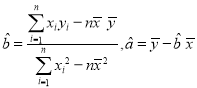 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com