
【题目】每年的4月23日为“世界读书日”,某调查机构对某校学生做了一个是否喜爱阅读的抽样调查.该调查机构从该校随机抽查了100名不同性别的学生(其中男生45名),统计了每个学生一个月的阅读时间,其阅读时间![]() (小时)的频率分布直方图如图所示:
(小时)的频率分布直方图如图所示:
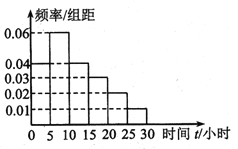
(1)求样本学生一个月阅读时间![]() 的中位数
的中位数![]() .
.
(2)已知样本中阅读时间低于![]() 的女生有30名,请根据题目信息完成下面的
的女生有30名,请根据题目信息完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
![]() 列联表
列联表
男 | 女 | 总计 | |
| |||
| |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
其中: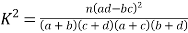 .
.
【答案】(1)![]() ;(2)不能在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
;(2)不能在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
【解析】
(1)频率为0.5对应的点的横坐标为中位数;
(2)100名学生中男生45名,女生55名,由频率分布直方图知,阅读时长大于等于![]() 的人数为50人,小于
的人数为50人,小于![]() 的也有50人,阅读时间低于
的也有50人,阅读时间低于![]() 的女生有30名,这样可得列联表中的各数,得列联表,依据
的女生有30名,这样可得列联表中的各数,得列联表,依据![]() 公式计算
公式计算![]() ,对照附表可得结论.
,对照附表可得结论.
(1)由题意得,直方图中第一组,第二组的频率之和为
![]() .
.
所以阅读时间的中位数![]() .
.
(2)由题意得,男生人数为45人,因此女生人数为55人,
由频率分布直方图知,阅读时长大于等于![]() 的人数为
的人数为![]() 人,
人,
故列联表补充如下:
男 | 女 | 总计 | |
| 25 | 25 | 50 |
| 20 | 30 | 50 |
总计 | 45 | 55 | 100 |
![]() 的观测值
的观测值![]()
![]() ,所以不能在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
,所以不能在犯错误的概率不超过0.1的前提下认为阅读与性别有关.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】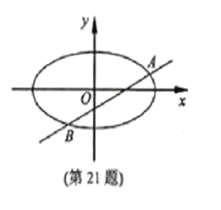
(本题满分15分)已知m>1,直线![]() ,
,
椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段
![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应国家号召,某校组织部分学生参与了“垃圾分类,从我做起”的知识问卷作答,并将学生的作答结果分为“合格”与“不合格”两类与“问卷的结果”有关?
不合格 | 合格 | |
男生 | 14 | 16 |
女生 | 10 | 20 |
(1)是否有90%以上的把握认为“性别”与“问卷的结果”有关?
(2)在成绩合格的学生中,利用性别进行分层抽样,共选取9人进行座谈,再从这9人中随机抽取5人发送奖品,记拿到奖品的男生人数为X,求X的分布列及数学期望![]() .
.
附: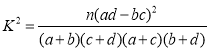
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.703 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对同学们而言,冬日的早晨离开暖融融的被窝,总是一个巨大的挑战,而咬牙起床的唯一动力,就是上学能够不迟到.己知学校要求每天早晨7:15之前到校,7:15之后到校记为迟到.小明每天6:15会被妈妈叫醒起味,吃早餐、洗漱等晨间活动需要半个小时,故每天6:45小明就可以出门去上学.从家到学校的路上,若小明选择步行到校,则路上所花费的时间相对准确,若以随机变量![]() (分钟)表示步行到校的时间,可以认为
(分钟)表示步行到校的时间,可以认为![]() .若小明选择骑共享单车上学,虽然骑行速度快于步行,不过由于车况、路况等不确定因素,路上所需时间的随机性增加,若以随机变量
.若小明选择骑共享单车上学,虽然骑行速度快于步行,不过由于车况、路况等不确定因素,路上所需时间的随机性增加,若以随机变量![]() (分钟)描述骑车到校的时间,可以认为
(分钟)描述骑车到校的时间,可以认为![]() .若小明选择坐公交车上学,速度很快,但是由于等车时间、路况等不确定因素,路上所需时间的随机性进一步增加,若以随机变量
.若小明选择坐公交车上学,速度很快,但是由于等车时间、路况等不确定因素,路上所需时间的随机性进一步增加,若以随机变量![]() (分钟)描述坐公交车到校所需的时间,则可以认为
(分钟)描述坐公交车到校所需的时间,则可以认为![]() .
.
(1)若某天小明妈妈出差没在家,小明一觉醒来已经是6:40了,他抓紧时间洗漱更衣,没吃早饭就出发了,出门时候是6:50.请问,小明是否有某种出行方案,能够保证上学不迟到?小明此时的最优选择是什么?
(2)已知共享单车每20分钟收费一元,若小明本周五天都骑共享单车上学,以随机变量![]() 表示这五天小明上学骑车的费用,求
表示这五天小明上学骑车的费用,求![]() 的期望与方差(此小题结果均保留三位有效数字)
的期望与方差(此小题结果均保留三位有效数字)
已知若随机变量![]() ,则
,则![]() %,
%,![]() %,
%,![]() %.
%.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将初始温度为![]() 的物体放在室温恒定为
的物体放在室温恒定为![]() 的实验室里,现等时间间隔测量物体温度,将第
的实验室里,现等时间间隔测量物体温度,将第![]() 次测量得到的物体温度记为
次测量得到的物体温度记为![]() ,已知
,已知![]() .已知物体温度的变化与实验室和物体温度差成正比(比例系数为
.已知物体温度的变化与实验室和物体温度差成正比(比例系数为![]() ).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
在上述模型下,设物体温度从![]() 升到
升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,那么
,那么![]() 与
与![]() 的大小关系是________(用“
的大小关系是________(用“![]() ”,“
”,“![]() ”或“
”或“![]() ”号填空)
”号填空)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com