
����Ŀ����ͬѧ�Ƕ��ԣ����յ��糿�뿪ů���ڵı��ѣ�����һ�������ս����ҧ����Ψһ������������ѧ�ܹ����ٵ�����֪ѧУҪ��ÿ���糿7:15֮ǰ��У��7:15֮��У��Ϊ�ٵ���С��ÿ��6:15�ᱻ���������ζ������͡�ϴ���ȳ�����Ҫ���Сʱ����ÿ��6:45С���Ϳ��Գ���ȥ��ѧ���Ӽҵ�ѧУ��·�ϣ���С��ѡ���е�У����·�������ѵ�ʱ�����ȷ�������������![]() �����ӣ���ʾ���е�У��ʱ�䣬������Ϊ
�����ӣ���ʾ���е�У��ʱ�䣬������Ϊ![]() ����С��ѡ���ﹲ��������ѧ����Ȼ�����ٶȿ��ڲ��У��������ڳ�����·���Ȳ�ȷ�����أ�·������ʱ�����������ӣ������������
����С��ѡ���ﹲ��������ѧ����Ȼ�����ٶȿ��ڲ��У��������ڳ�����·���Ȳ�ȷ�����أ�·������ʱ�����������ӣ������������![]() �����ӣ������ﳵ��У��ʱ�䣬������Ϊ
�����ӣ������ﳵ��У��ʱ�䣬������Ϊ![]() ����С��ѡ������������ѧ���ٶȺܿ죬�������ڵȳ�ʱ�䡢·���Ȳ�ȷ�����أ�·������ʱ�������Խ�һ�����ӣ������������
����С��ѡ������������ѧ���ٶȺܿ죬�������ڵȳ�ʱ�䡢·���Ȳ�ȷ�����أ�·������ʱ�������Խ�һ�����ӣ������������![]() �����ӣ���������������У�����ʱ�䣬�������Ϊ
�����ӣ���������������У�����ʱ�䣬�������Ϊ![]() ��
��
��1����ij��С���������û�ڼң�С��һ�������Ѿ���6:40�ˣ���ץ��ʱ��ϴ�����£�û���緹�ͳ����ˣ�����ʱ����6:50�����ʣ�С���Ƿ���ij�ֳ��з������ܹ���֤��ѧ���ٵ���С����ʱ������ѡ����ʲô��
��2����֪��������ÿ20�����շ�һԪ����С���������춼�ﹲ��������ѧ�����������![]() ��ʾ������С����ѧ�ﳵ�ķ��ã���
��ʾ������С����ѧ�ﳵ�ķ��ã���![]() �������뷽���С������������λ��Ч���֣�
�������뷽���С������������λ��Ч���֣�
��֪���������![]() ����
����![]() ����
����![]() ����
����![]() ����
����
���𰸡���1�������ַ�����������![]() ԭ���ܱ�֤��ѧ���ٵ�����Զ��ԣ��ﳵ��У���ٵ��ĸ�����ߣ�������ѡ��2��
ԭ���ܱ�֤��ѧ���ٵ�����Զ��ԣ��ﳵ��У���ٵ��ĸ�����ߣ�������ѡ��2��![]() ��Ԫ����
��Ԫ����![]() ��Ԫ2��
��Ԫ2��
��������
��1�������⣬С����Ҫ��25�����ڵ���ѧУ������ѡ���е�У���ٵ��ĸ��ʼ�Ϊ![]() �����
�����![]() �������ﳵ��У���ٵ����ʼ�Ϊ
�������ﳵ��У���ٵ����ʼ�Ϊ![]() ��
��
![]() ��
��![]() ����
����![]() ������������������У���ٵ��ĸ��ʼ�Ϊ
������������������У���ٵ��ĸ��ʼ�Ϊ![]() ��
��
![]() �����Ƚϼ�������ѡ��2��ȡ�������
�����Ƚϼ�������ѡ��2��ȡ�������![]() ��ʾ�������ﳵ��ѧʱ�䵥�̳���20���ӵ������������
��ʾ�������ﳵ��ѧʱ�䵥�̳���20���ӵ������������![]() ��
��![]() ������
������![]() �������뷽��.
�������뷽��.
��1�������⣬С����Ҫ��25�����ڵ���ѧУ��
����ѡ���е�У���ٵ��ĸ��ʼ�Ϊ![]() ��ȡ
��ȡ![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ����
����
���ﳵ��У���ٵ��ĸ��ʼ�Ϊ![]() ��ȡ
��ȡ![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ����
����
![]() ����
����
��![]() ��
��![]() ����
����![]() ����
����
������������У���ٵ��ĸ��ʼ�Ϊ![]() ��ȡ
��ȡ![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ����
����
���ϣ����ַ�����������![]() ԭ���ܱ�֤��ѧ���ٵ�����Զ��ԣ��ﳵ��У���ٵ��ĸ�����ߣ�������ѡ��
ԭ���ܱ�֤��ѧ���ٵ�����Զ��ԣ��ﳵ��У���ٵ��ĸ�����ߣ�������ѡ��
��2��ȡ�������![]() ��ʾ�������ﳵ��ѧʱ�䵥�̳���20���ӵ�������
��ʾ�������ﳵ��ѧʱ�䵥�̳���20���ӵ�������
�����⣬ÿ���ﳵ��ѧʱ�䳬��20���ӵĸ���Ϊ![]() ����
����
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
�֡�![]() ��
��
��![]() ��Ԫ����
��Ԫ����![]() ��Ԫ2��
��Ԫ2��


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ֲ��â���ٽ�����ʱ�������һЩâ������ժ��100��â�����������ֱ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����λ���ˣ��У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
����λ���ˣ��У���ͳ�Ƶ�Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.
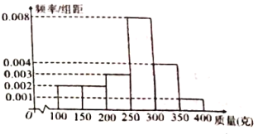
��1������������������ݵ���λ����
��2���ְ��ֲ����������Ϊ![]() ��
��![]() ��â���������ȡ6�����ٴ���6���������ȡ3��������3��â����ǡ��1����
��â���������ȡ6�����ٴ���6���������ȡ3��������3��â����ǡ��1����![]() �ڵĸ���.
�ڵĸ���.
��3��ij���������չ�â�����Ը������ݵ��м��������������ݵ�ƽ��ֵ���������������壬����ֲ�л�δժ�µ�â����Լ����10000����������������������չ�������
A������â����10Ԫ/ǧ���չ���
B������������250�˵�â����2Ԫ/���չ������ڻ����250�˵���3Ԫ/���չ���ͨ������ȷ����ֲѡ�����ַ����������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ�����Σ�
������![]() ����
����![]() ��
��![]() ��
��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() �ϵĶ��㣨����
�ϵĶ��㣨����![]() ��.
��.
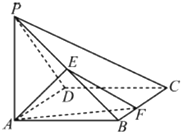
��1��ƽ��![]() ��ƽ��
��ƽ��![]() �Ƿ��ഹֱ������ǣ���֤����������ǣ���˵�����ɣ�
�Ƿ��ഹֱ������ǣ���֤����������ǣ���˵�����ɣ�
��2��������![]() ������ֵ��ȡֵ��Χ.
������ֵ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���4��23��Ϊ���������������ij���������ijУѧ������һ���Ƿ�ϲ���Ķ��ij�������.�õ�������Ӹ�У��������100����ͬ�Ա��ѧ������������45������ͳ����ÿ��ѧ��һ���µ��Ķ�ʱ�䣬���Ķ�ʱ��![]() ��Сʱ����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
��Сʱ����Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
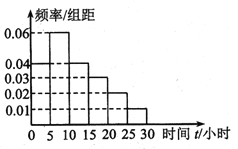
��1��������ѧ��һ�����Ķ�ʱ��![]() ����λ��
�����![]() .
.
��2����֪�������Ķ�ʱ�����![]() ��Ů����30�����������Ŀ��Ϣ��������
��Ů����30�����������Ŀ��Ϣ��������![]() �����������ж��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ�Ķ����Ա��й�.
�����������ж��ܷ��ڷ�����ĸ��ʲ�����0.1��ǰ������Ϊ�Ķ����Ա��й�.
![]() ������
������
�� | Ů | �ܼ� | |
| |||
| |||
�ܼ� |
������
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
����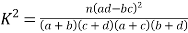 .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() ��
�� ![]() ��
��![]() ��.
��.
��1����![]() ʱ��������
ʱ��������![]() ��
��![]() ��ͼ����
��ͼ����![]() ������ͬ�����ߣ���
������ͬ�����ߣ���![]() ��ֵ��
��ֵ��
��2����![]() ʱ����������
ʱ����������![]() ������
������![]() ���ܴ��ڲ���ȵ���ʵ��
���ܴ��ڲ���ȵ���ʵ��![]() ��ʹ��
��ʹ��![]() ����
����![]() ����Сֵ��
����Сֵ��
��3����![]() ʱ���躯��
ʱ���躯��![]() ��
��![]() ��ͼ����
��ͼ����![]()
![]() ���㣮��֤��
���㣮��֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������{an}��an��Z����ǰn���ΪSn����S1��S2������Sn�������ĸ���Ϊbn��
��1����an=n����д������{bn}��ǰ5�
��2����֤����a1Ϊ������ai��i=2��3��4������Ϊż������������{bn}�ǵ��������������ij�ֲ���Ҫ������
��3����ai=bi��i=1��2��3������������{an}��ͨ�ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P���ⳤΪ1��������ABCD��A1B1C1D1�ĵ���A1B1C1D1��һ�㣬��![]() ��ȡֵ��Χ��__.
��ȡֵ��Χ��__.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��ֱ��l����������ԭ��O�Ҳ�ƽ���������ᣬl��
��ֱ��l����������ԭ��O�Ҳ�ƽ���������ᣬl��![]() �ཻ��A��B���㣬�߶�
�ཻ��A��B���㣬�߶�![]() ���е�ΪM.
���е�ΪM.
��1��֤����ֱ��![]() ��б����ֱ��l��б�ʵij˻�Ϊ��ֵ��
��б����ֱ��l��б�ʵij˻�Ϊ��ֵ��
��2����ֱ��l����![]() ���ӳ���
���ӳ���![]() ��
��![]() ���ڵ�P�����ı���
���ڵ�P�����ı���![]() ��ƽ���ı��Σ���ֱ��l��б�ʣ�
��ƽ���ı��Σ���ֱ��l��б�ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com