
【题目】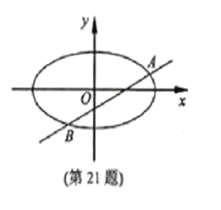
(本题满分15分)已知m>1,直线![]() ,
,
椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段
![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面上的一列点![]() 简记为
简记为![]() ,若由
,若由![]() 构成的数列
构成的数列![]() 满足
满足![]() ,(其中
,(其中![]() 是与
是与![]() 轴正方向相同的单位向量),则称
轴正方向相同的单位向量),则称![]() 为“
为“![]() 点列”.
点列”.
(1)试判断:![]() ,...是否为“
,...是否为“![]() 点列”?并说明理由.
点列”?并说明理由.
(2)若![]() 为“
为“![]() 点列”,且点
点列”,且点![]() 在点
在点![]() 的右上方.任取其中连续三点
的右上方.任取其中连续三点![]() ,判断
,判断![]() 的形状(锐角,直角,钝角三角形),并证明.
的形状(锐角,直角,钝角三角形),并证明.
(3)若![]() 为“
为“![]() 点列”,正整数
点列”,正整数![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某游戏厂商对新出品的一款游戏设定了“防沉迷系统”,规则如下:
①3小时以内(含3小时)为健康时间,玩家在这段时间内获得的累积经验值![]() 单位:
单位:![]() 与游玩时间
与游玩时间![]() 小时)满足关系式:
小时)满足关系式:![]() ;
;
②3到5小时(含5小时)为疲劳时间,玩家在这段时间内获得的经验值为![]() 即累积经验值不变);
即累积经验值不变);
③超过5小时为不健康时间,累积经验值开始损失,损失的经验值与不健康时间成正比例关系,比例系数为50.
⑴当![]() 时,写出累积经验值E与游玩时间t的函数关系式
时,写出累积经验值E与游玩时间t的函数关系式![]() ,并求出游玩6小时的累积经验值;
,并求出游玩6小时的累积经验值;
⑵该游戏厂商把累积经验值E与游玩时间t的比值称为“玩家愉悦指数”,记作![]() ;若
;若![]() ,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
,且该游戏厂商希望在健康时间内,这款游戏的“玩家愉悦指数”不低于24,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
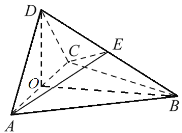
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是由非负整数组成的无穷数列,对每一个正整数
是由非负整数组成的无穷数列,对每一个正整数![]() ,该数列前
,该数列前![]() 项的最大值记为
项的最大值记为![]() ,第
,第![]() 项之后各项
项之后各项![]() 的最小值记为
的最小值记为![]() ,记
,记![]() .
.
(1)若数列![]() 的通项公式为
的通项公式为![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)证明:“数列![]() 单调递增”是“
单调递增”是“![]() ”的充要条件;
”的充要条件;
(3)若![]() 对任意
对任意![]() 恒成立,证明:数列
恒成立,证明:数列![]() 的通项公式为
的通项公式为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 上一点,经过点
上一点,经过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点(不同于点
两点(不同于点![]() ),直线
),直线![]() 、
、![]() 分别交直线
分别交直线![]() 于点
于点![]() 、
、![]() .
.
(1)求抛物线方程及其焦点坐标;
(2)求证:以![]() 为直径的圆恰好经过原点.
为直径的圆恰好经过原点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖活动,抽奖箱中放有编号分别为![]() 的五个小球.小球除编号不同外,其余均相同.活动规则如下:从抽奖箱中随机抽取一球,若抽到的小球编号为
的五个小球.小球除编号不同外,其余均相同.活动规则如下:从抽奖箱中随机抽取一球,若抽到的小球编号为![]() ,则获得奖金
,则获得奖金![]() 元;若抽到的小球编号为偶数,则获得奖金
元;若抽到的小球编号为偶数,则获得奖金![]() 元;若抽到其余编号的小球,则不中奖.现某顾客依次有放回的抽奖两次.
元;若抽到其余编号的小球,则不中奖.现某顾客依次有放回的抽奖两次.
(1)求该顾客两次抽奖后都没有中奖的概率;
(2)求该顾客两次抽奖后获得奖金之和为![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com