
【题目】设椭圆![]() (
(![]() )的左、右焦点为
)的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .已知
.已知![]() .
.
(1)求椭圆的离心率;
(2)设![]() 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段![]() 为直径的圆经过点
为直径的圆经过点![]() ,经过原点
,经过原点![]() 的直线
的直线![]() 与该圆相切,求直线
与该圆相切,求直线![]() 的斜率.
的斜率.
【答案】(1)![]() ;(2)直线
;(2)直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.
【解析】试题(1)设椭圆的右焦点![]() 的坐标为
的坐标为![]() ,由已知
,由已知![]() ,可得
,可得![]() ,结合
,结合![]() ,可得
,可得![]() ,从而可求得椭圆的离心率;(2)在(1)的基础上,可先利用
,从而可求得椭圆的离心率;(2)在(1)的基础上,可先利用![]() 及数量积的坐标运算求出
及数量积的坐标运算求出![]() 点的坐标,再求出以线段
点的坐标,再求出以线段![]() 为直径的圆的方程(圆心坐标和半径),最后设经过原点
为直径的圆的方程(圆心坐标和半径),最后设经过原点![]() 的与该圆相切的直线
的与该圆相切的直线![]() 的方程为
的方程为![]() ,由圆心到切线的距离等于半径,列方程,解方程即可得求得直线
,由圆心到切线的距离等于半径,列方程,解方程即可得求得直线![]() 的斜率.
的斜率.
(1)设椭圆的右焦点![]() 的坐标为
的坐标为![]() .由
.由![]() ,可得
,可得![]() ,又
,又![]() ,则
,则![]() ,∴椭圆的离心率
,∴椭圆的离心率![]() .
.
(2)由(1)知![]() ,
, ![]() ,故椭圆方程为
,故椭圆方程为![]() .设
.设![]() .由
.由![]() ,
, ![]() ,有
,有![]() ,
, ![]() .由已知,有
.由已知,有![]() ,即
,即![]() .又
.又![]() ,故有
,故有![]() ①
①
又∵点![]() 在椭圆上,故
在椭圆上,故![]() ②
②
由①和②可得![]() .而点
.而点![]() 不是椭圆的顶点,故
不是椭圆的顶点,故![]() ,代入①得
,代入①得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .设圆的圆心为
.设圆的圆心为![]() ,则
,则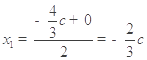 ,
,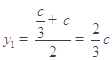 ,进而圆的半径
,进而圆的半径![]() .设直线
.设直线![]() 的斜率为
的斜率为![]() ,依题意,直线
,依题意,直线![]() 的方程为
的方程为![]() .由
.由![]() 与圆相切,可得
与圆相切,可得![]() ,即
,即 ,整理得
,整理得![]() ,解得
,解得![]() .∴直线
.∴直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,A 为椭圆![]() 的下顶点,过 A 的直线 l 交抛物线
的下顶点,过 A 的直线 l 交抛物线![]() 于B、C 两点,C 是 AB 的中点.
于B、C 两点,C 是 AB 的中点.
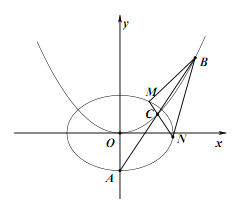
(I)求证:点C的纵坐标是定值;
(II)过点C作与直线 l 倾斜角互补的直线l交椭圆于M、N两点,求p的值,使得△BMN的面积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,其峰值理论传输速度可达每8秒1GB,比4G网络的传输速度快数百倍.举例来说,一部1G的电影可在8秒之内下载完成.随着5G技术的诞生,用智能终端分享3D电影、游戏以及超高画质(UHD)节目的时代正向我们走来.某手机网络研发公司成立一个专业技术研发团队解决各种技术问题,其中有数学专业毕业,物理专业毕业,其它专业毕业的各类研发人员共计1200人.现在公司为提高研发水平,采用分层抽样抽取400人按分数对工作成绩进行考核,并整理得如上频率分布直方图(每组的频率视为概率).

(1)从总体的1200名学生中随机抽取1人,估计其分数小于50的概率;
(2)研发公司决定对达到某分数以上的研发人员进行奖励,要求奖励研发人员的人数达到30%,请你估计这个分数的值;
(3)已知样本中有三分之二的数学专业毕业的研发人员分数不低于70分,样本中不低于70分的数学专业毕业的研发人员人数与物理及其它专业毕业的研发人员的人数和相等,估计总体中数学专业毕业的研发人员的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】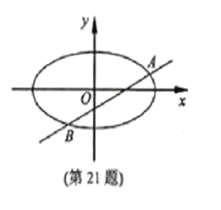
(本题满分15分)已知m>1,直线![]() ,
,
椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段
![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com