
【题目】将初始温度为![]() 的物体放在室温恒定为
的物体放在室温恒定为![]() 的实验室里,现等时间间隔测量物体温度,将第
的实验室里,现等时间间隔测量物体温度,将第![]() 次测量得到的物体温度记为
次测量得到的物体温度记为![]() ,已知
,已知![]() .已知物体温度的变化与实验室和物体温度差成正比(比例系数为
.已知物体温度的变化与实验室和物体温度差成正比(比例系数为![]() ).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
).给出以下几个模型,那么能够描述这些测量数据的一个合理模型为__________:(填写模型对应的序号)
①![]() ;②
;②![]() ;③
;③![]() .
.
在上述模型下,设物体温度从![]() 升到
升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,从
,从![]() 上升到
上升到![]() 所需时间为
所需时间为![]() ,那么
,那么![]() 与
与![]() 的大小关系是________(用“
的大小关系是________(用“![]() ”,“
”,“![]() ”或“
”或“![]() ”号填空)
”号填空)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】每年的4月23日为“世界读书日”,某调查机构对某校学生做了一个是否喜爱阅读的抽样调查.该调查机构从该校随机抽查了100名不同性别的学生(其中男生45名),统计了每个学生一个月的阅读时间,其阅读时间![]() (小时)的频率分布直方图如图所示:
(小时)的频率分布直方图如图所示:
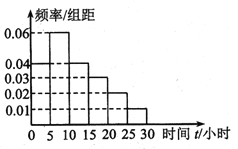
(1)求样本学生一个月阅读时间![]() 的中位数
的中位数![]() .
.
(2)已知样本中阅读时间低于![]() 的女生有30名,请根据题目信息完成下面的
的女生有30名,请根据题目信息完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
列联表,并判断能否在犯错误的概率不超过0.1的前提下认为阅读与性别有关.
![]() 列联表
列联表
男 | 女 | 总计 | |
| |||
| |||
总计 |
附表:
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
其中: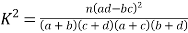 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线l不经过坐标原点O且不平行与坐标轴,l与
,直线l不经过坐标原点O且不平行与坐标轴,l与![]() 相交于A,B两点,线段
相交于A,B两点,线段![]() 的中点为M.
的中点为M.
(1)证明:直线![]() 的斜率与直线l的斜率的乘积为定值;
的斜率与直线l的斜率的乘积为定值;
(2)若直线l过点![]() ,延长线
,延长线![]() 与
与![]() 交于点P,若四边形
交于点P,若四边形![]() 是平行四边形,求直线l的斜率;
是平行四边形,求直线l的斜率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
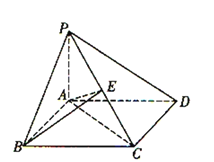
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com