练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

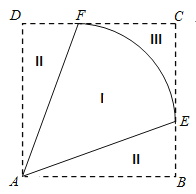
    【题目】某地拟规划种植一批芍药，为了美观，将种植区域（区域I）设计成半径为1km的扇形，中心角（）.为方便观赏，增加收入，在种植区域外围规划观赏区（区域II）和休闲区（区域III），并将外围区域按如图所示的方案扩建成正方形，其中点，分别在边和上．已知种植区、观赏区和休闲区每平方千米的年收入分别是10万元、20万元、20万元.

    （1）要使观赏区的年收入不低于5万元，求的最大值；

    （2）试问：当为多少时，年总收入最大？

    【答案】（1）（2）

    【解析】

    （1）由，，，所以与全等.

    可得，根据面积公式，可求得观赏区的面积为，要使得观赏区的年收入不低于5万元，则要求，解不等式即可求出结果.

    （2）由题意可得种植区的面积为，正方形面积为，设年总收入为万元，则

    ，利用导数在函数单调性中的应用，即可求出结果.

    （1）∵，，，所以与全等.

    所以，观赏区的面积为

    ，要使得观赏区的年收入不低于5万元，则要求，即，结合可知，则的最大值为.

    （2）种植区的面积为，

    正方形面积为，

    设年总收入为万元，则

    ，

    其中，求导可得.

    当时，，递增；当时，，递增.

    所以当时，取得最大值，此时年总收入最大.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为、，离心率，点在椭圆上.

    （1）求椭圆的方程；

    （2）设过点且不与坐标轴垂直的直线交椭圆于、两点，线段的垂直平分线与轴交于点，求点的横坐标的取值范围；

    （3）在第（2）问的条件下，求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，曲线在点处的切线方程为．

    （1）求，的值；

    （2）若，求函数的单调区间；

    （3）设函数，且在区间内存在单调递减区间，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线的焦点F（1，0），O为坐标原点，A，B是抛物线C上异于 O的两点．

    （1）求抛物线C的方程；

    （2）若直线AB过点（8，0），求证：直线OA，OB的斜率之积为定值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数.

    （1）若对定义域内的任意，都有成立，求实数的值；

    （2）若函数的定义域上是单调函数，求实数的取值范围；

    （3）若，证明对任意的正整数， .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面四个正方体图形中，、为正方体的两个顶点，、、分别为其所在棱的中点，能得出平面的图形是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过点，且离心率为．

    （Ⅰ）求椭圆的方程；

    （Ⅱ）设是椭圆上的点，直线与（为坐标原点）的斜率之积为．若动点满足，试探究是否存在两个定点，使得为定值？若存在，求的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

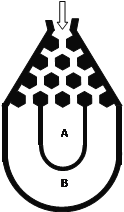
    【题目】(本题满分12分)将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中,将3次遇到黑色障碍物,最后落入袋或袋中.已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是.

    （Ⅰ）求小球落入袋中的概率;

    （Ⅱ）在容器入口处依次放入4个小球,记为落入袋中小球的个数,试求的概率和的数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，平面，四边形是菱形，，，是上任意一点。

    （1）求证：；

    （2）当面积的最小值是9时，在线段上是否存在点，使与平面所成角的正切值为2？若存在？求出的值，若不存在，请说明理由

    查看答案和解析>>

    同步练习册答案