
【题目】设函数![]() .
.
(1)若对定义域内的任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的值;
的值;
(2)若函数![]() 的定义域上是单调函数,求实数
的定义域上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若![]() ,证明对任意的正整数
,证明对任意的正整数![]() ,
, ![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)由![]() ,得
,得![]() 的定义域为
的定义域为![]() ,因为对
,因为对![]() ,都有
,都有![]() 成立,所以
成立,所以![]() 是函数
是函数![]() 的最小值,所以
的最小值,所以![]() ,即可求解
,即可求解![]() 的值;(2)由
的值;(2)由![]() ,函数
,函数![]() 在定义域上单调函数,知
在定义域上单调函数,知![]() 或
或![]() 在
在![]() 上恒成立,由此能求出实数
上恒成立,由此能求出实数![]() 的取值范围;(3)当
的取值范围;(3)当![]() 时,函数
时,函数![]() ,令
,令![]() ,
,
则![]() ,由此入手能够证明
,由此入手能够证明![]() .
.
试题解析:(1)由![]() ,得
,得![]() .∴
.∴![]() 的定义域为
的定义域为![]() .
.
因为对x∈![]() ,都有
,都有![]() ,∴
,∴![]() 是函数
是函数![]() 的最小值,故有
的最小值,故有![]() .
.
![]() 解得
解得![]() .
.
经检验,![]() 时,
时,![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增.
上单调增.![]() 为最小值.故得证.
为最小值.故得证.
(2)∵![]() 又函数
又函数![]() 在定义域上是单调函数,
在定义域上是单调函数,
∴![]() 或
或![]() 在
在![]() 上恒成立.
上恒成立.
若![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
即![]() =
=![]() 恒成立,由此得
恒成立,由此得![]()
![]() ;
;
若![]() ,则
,则![]() 在
在![]() 上恒成立,
上恒成立,
即![]() =
=![]() 恒成立.
恒成立.
因![]() 在
在![]() 上没有最小值,∴不存在实数
上没有最小值,∴不存在实数![]() 使
使![]() 恒成立.
恒成立.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
(3)当![]() 时,函数
时,函数![]() .
.
令![]() ,
,
则![]() .
.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() 当
当![]() 时,恒有
时,恒有![]() ,即
,即![]() 恒成立.
恒成立.
故当![]() 时,有
时,有![]() .
.
而![]() ,
,![]() .取
.取![]() ,则有
,则有![]() .
.
![]()
![]() .所以结论成立.
.所以结论成立.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等(如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
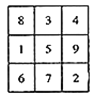
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将集合M={1,2,3,...,15}表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为________;请写出满足上述条件的集合M的5个三元子集__________(只写出一组)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为
的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元)
(单位:元)
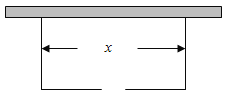
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)若曲线![]() 的一条切线经过点
的一条切线经过点![]() ,求这条切线的方程.
,求这条切线的方程.
(2)若关于![]() 的方程
的方程![]() 有两个不相等的实数根x1,x2。
有两个不相等的实数根x1,x2。
①求实数a的取值范围;
②证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD, ![]() ,M为PC的中点,N点在AB上且
,M为PC的中点,N点在AB上且![]() .
.
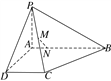
(1)证明:MN∥平面PAD;
(2)求直线MN与平面PCB所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com