
【题目】已知抛物线![]() 的焦点为
的焦点为![]() .
.
(1)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)点![]() 是抛物线
是抛物线![]() 上的两点,点
上的两点,点![]() 的纵坐标分别为1,2,分别过点
的纵坐标分别为1,2,分别过点![]() 作倾斜角互补的两条直线交抛物线
作倾斜角互补的两条直线交抛物线![]() 于另外不同两点
于另外不同两点![]() ,求直线
,求直线![]() 的斜率.
的斜率.
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,将直线与抛物线联立消去
,将直线与抛物线联立消去![]() ,根据韦达定理可得
,根据韦达定理可得![]() ,
,![]() ,再由抛物线定义可得
,再由抛物线定义可得![]() 即可求解.
即可求解.
(2)求出点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,分类讨论①当两条直线的倾斜角都为
,分类讨论①当两条直线的倾斜角都为![]() 时,②当两条直线的倾斜角都不为
时,②当两条直线的倾斜角都不为![]() 时,设直线
时,设直线![]() 的方程与设直线
的方程与设直线![]() 的方程,分别将直线与抛物线联立,利用韦达定理,整理化简即可求出直线
的方程,分别将直线与抛物线联立,利用韦达定理,整理化简即可求出直线![]() 的斜率.
的斜率.
(1)设直线![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
联立方程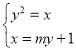 ,消去
,消去![]() 整理为
整理为![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,
由抛物线定义可得![]() ,
,![]() ,所以
,所以![]() ,
,
解得:![]() ,
,
故直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
(2)由题意知,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
①当两条直线的倾斜角都为![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
此时直线![]() 的斜率为
的斜率为![]() ,
,
②当两条直线的倾斜角都不为![]() 时,设点
时,设点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
此时直线![]() 的斜率为
的斜率为![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
联立方程![]() 消去
消去![]() 整理为
整理为![]() ,则
,则![]() ,得
,得![]() ,
,
设直线![]() 的方程为
的方程为![]() ,
,
联立方程![]() 消去
消去![]() 整理为
整理为![]() ,
,
则![]() ,得
,得![]() ,
,
所以![]() ,可得
,可得![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,
,
综上,可得直线![]() 的斜率为
的斜率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知无穷数列{an}(an∈Z)的前n项和为Sn,记S1,S2,…,Sn中奇数的个数为bn.
(1)若an=n,请写出数列{bn}的前5项;
(2)求证:“a1为奇数,ai(i=2,3,4,…)为偶数”是“数列{bn}是单调递增数列”的充分不必要条件;
(3)若ai=bi,i=1,2,3,…,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线l不经过坐标原点O且不平行与坐标轴,l与
,直线l不经过坐标原点O且不平行与坐标轴,l与![]() 相交于A,B两点,线段
相交于A,B两点,线段![]() 的中点为M.
的中点为M.
(1)证明:直线![]() 的斜率与直线l的斜率的乘积为定值;
的斜率与直线l的斜率的乘积为定值;
(2)若直线l过点![]() ,延长线
,延长线![]() 与
与![]() 交于点P,若四边形
交于点P,若四边形![]() 是平行四边形,求直线l的斜率;
是平行四边形,求直线l的斜率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,射线
中,射线![]() 的方程为
的方程为![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的方程为
的方程为![]() .一只小虫从点
.一只小虫从点![]() 沿射线
沿射线![]() 向上以
向上以![]() 单位/min的速度爬行
单位/min的速度爬行
(1)以小虫爬行时间![]() 为参数,写出射线
为参数,写出射线![]() 的参数方程;
的参数方程;
(2)求小虫在曲线![]() 内部逗留的时间.
内部逗留的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在常数a,使得数列{an}满足:若x是数列{an}中的一项,则a-x也是数列{an}中的一项,称数列{an}为“兑换数列”,常数a是它的“兑换系数”.
(1)若数列:2,3,6,m(m>6)是“兑换系数”为a的“兑换数列”,求m和a的值;
(2)已知有穷等差数列{bn}的项数是n0(n0≥3),所有项之和是B,求证:数列{bn}是“兑换数列”,并用n0和B表示它的“兑换系数”;
(3)对于一个不少于3项,且各项皆为正整数的递增数列{cn},是否有可能它既是等比数列,又是“兑换数列”?给出你的结论,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立七十周年,新中国成立以来,我国文化事业得到了充分发展,尤其是党的十八大以来,文化事业发展更加迅速,下图是从2013 年到 2018 年六年间我国公共图书馆业机构数(个)与对应年份编号的散点图(为便于计算,将 2013 年编号为 1,2014 年编号为 2,…,2018年编号为 6,把每年的公共图书馆业机构个数作为因变量,把年份编号从 1 到 6 作为自变量进行回归分析),得到回归直线![]() ,其相关指数
,其相关指数![]() ,给出下列结论,其中正确的个数是( )
,给出下列结论,其中正确的个数是( )

①公共图书馆业机构数与年份的正相关性较强
②公共图书馆业机构数平均每年增加13.743个
③可预测 2019 年公共图书馆业机构数约为3192个
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】惠州市某商店销售某海鲜,经理统计了春节前后50天该海鲜的日需求量![]() (
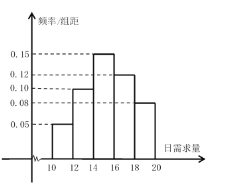
(![]() ,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为
,单位:公斤),其频率分布直方图如下图所示.该海鲜每天进货1次,每销售1公斤可获利40元;若供大于求,剩余的海鲜削价处理,削价处理的海鲜每公斤亏损10元;若供不应求,可从其它商店调拨,调拨的海鲜销售1公斤可获利30元.假设商店该海鲜每天的进货量为14公斤,商店销售该海鲜的日利润为![]() 元.
元.
(1)求商店日利润![]() 关于日需求量
关于日需求量![]() 的函数表达式.
的函数表达式.
(2)根据频率分布直方图,
①估计这50天此商店该海鲜日需求量的平均数.
②假设用事件发生的频率估计概率,请估计日利润不少于620元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com