
分析 (1)根据题意,先选出A、B,再从其它10个人中再选3人即可,由组合数公式计算可得答案;
(2)根据题意,只需从其它10人中任选5人即可,由组合数公式计算可得答案;
(3)根据题意,按A、B的选取情况进行分类:①,A、B全不选,②,A、B中选1人,先求出每种情况的选法数目,再由分类计数原理计算可得答案;
(4)根据题意,用间接法,先计算从12人中任选5人的选法数目,再分别计算①没有女学生入选,②只有1名女生入选,在总数中将其排除即可得答案;
(5)根据题意,分3步进行,①选出一个男生担任体育班委,②再选出1名女生担任文娱班委,③剩下名6男生再选2人,4名女生中再选取1人,任其它3个班委,先求出每一步的选法数目,再用分步计数原理可得即可得答案
解答 解:(1)根据题意,先选出A、B,再从其它10个人中再选3人即可,共有的选法种数为C103=120种,
(2)根据题意,A、B都不当选,只需从其它10人中任选5人即可,共有的选法种数为C105=252种:
(3)根据题意,按A、B的选取情况进行分类:
①,A、B全不选的方法数为C105=252种,
②,A、B中选1人的方法数为C21C104=420,
共有选法252+420=672种,
(4)根据题意,从12人中任选5人,有C125种选法,
没有女学生入选,即全选男生的情况有C75种情况,
只有1名女生入选,即选取1女4男,有C51×C74种选法,
故所有符合条件选法数为:C125-C75-C51×C74=596种,
(5)选出一个男生担任体育班委,有C71种情况,
再选出1名女生担任文娱班委,有C51种情况,
剩下名6男生再选2人,4名女生中再选取1人,任其它3个班委,有C62×C41×A33种情况,
用分步计数原理可得到所有方法总数为:C71×C51×C62×C41×A33=12600种.
点评 本题考查排列、组合的应用,涉及分类、分步计数原理的运用,解(4)题时注意间接方法的运用,可以避免分类讨论.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:(x+$\sqrt{3}$)2+y2=16,点F($\sqrt{3}$,0),P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{4}$,$\frac{π}{4}$] | C. | [$\frac{π}{6}$,$\frac{2π}{3}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.
如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
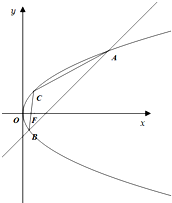 已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.
已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com