
分析 先计算n=1,2,3,4的结果,根据计算结果的规律进行猜想,然后使用数学归纳法证明.
解答 解:n=1时,$\frac{1}{1×3}=\frac{1}{3}$,
n=2时,$\frac{1}{1×3}+\frac{1}{3×5}$=$\frac{2}{5}$,
n=3时,$\frac{1}{1×3}+\frac{1}{3×5}$+$\frac{1}{5×7}$=$\frac{3}{7}$,
n=4时,$\frac{1}{1×3}+\frac{1}{3×5}$+$\frac{1}{5×7}$+$\frac{1}{7×9}$=$\frac{4}{9}$,
猜想:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$=$\frac{n}{2n+1}$.
证明:(1)当n=1时,$\frac{1}{1×3}$=$\frac{1}{3}$,猜想成立.
(2)假设n=k(k∈N+)时猜想成立,即有$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2k-1)(2k+1)}$=$\frac{k}{2k+1}$,
则当n=k+1时,
$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2k-1)(2k+1)}$+$\frac{1}{(2k+1)(2k+3)}$
=$\frac{k}{2k+1}$+$\frac{1}{(2k+1)(2k+3)}$=$\frac{k(2k+3)+1}{(2k+1)(2k+3)}$
=$\frac{{2{k^2}+3k+1}}{(2k+1)(2k+3)}$
=$\frac{(k+1)(2k+1)}{(2k+1)(2k+3)}$
=$\frac{k+1}{2k+3}$
=$\frac{k+1}{2(k+1)+1}$,
所以当n=k+1时,猜想成立.
由(1)(2)可知,对一切n∈N+猜想成立.即$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$=$\frac{n}{2n+1}$.
点评 本题考查了归纳推理,数学归纳法证明,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1} | C. | [0,1] | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\left\{\begin{array}{l}{{x}^{2}+3x+4(x<0)}\\{{x}^{2}-3x+4(x≥0)}\end{array}\right.$ | B. | f(x)=$\left\{\begin{array}{l}{{x}^{2}-3x+4(x<0)}\\{{x}^{2}+3x+4(x≥0)}\end{array}\right.$ | ||
| C. | f(x)=$\left\{\begin{array}{l}{{x}^{2}+3x-4(x<0)}\\{{x}^{2}-3x-4(x≥0)}\end{array}\right.$ | D. | f(x)=$\left\{\begin{array}{l}{{x}^{2}-3x-4(x<0)}\\{{x}^{2}+3x-4(x≥0)}\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ex | B. | y=sin2x | C. | y=-x3 | D. | y=log${\;}_{\frac{1}{2}}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
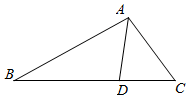 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com