
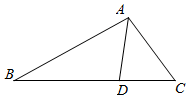
 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.分析 (Ⅰ)由平方关系求出sin∠ADB的值,由图象和两角差的正弦公式求出sinC的值;
(Ⅱ)由(I)和正弦定理求出AD的长,代入三角形的面积公式求出△ABD的面积.
解答 解:(Ⅰ)在△ABC中,因为$cos∠ADB=-\frac{{\sqrt{2}}}{10}$,且∠ADB∈(0,π),(1分)
所以$sin∠ADB=\sqrt{1-{{cos}^2}∠ADB}=\frac{{7\sqrt{2}}}{10}$.(2分)
因为$∠CAD=\frac{π}{4}$,所以$C=∠ADB-\frac{π}{4}$.(3分)
所以$sinC=sin(∠ADB-\frac{π}{4})=sin∠ADB•cos\frac{π}{4}-cos∠ADB•sin\frac{π}{4}$(5分)
=$\frac{{7\sqrt{2}}}{10}×\frac{{\sqrt{2}}}{2}+\frac{{\sqrt{2}}}{10}×\frac{{\sqrt{2}}}{2}=\frac{4}{5}$.(6分)
(Ⅱ)在△ACD中,由正弦定理得$\frac{AD}{sinC}=\frac{AC}{sin∠ADC}$,(7分)
所以AD=$\frac{AC•sinC}{sin∠ADC}$=$\frac{7×\frac{4}{5}}{\frac{7\sqrt{2}}{10}}$=4$\sqrt{2}$,(9分),
所以${S_{△ABD}}=\frac{1}{2}AD•BD•sin∠ADB=\frac{1}{2}×4\sqrt{2}×10×\frac{{7\sqrt{2}}}{10}=28$.(12分)
点评 本题考查正弦定理,两角差的正弦公式,以及三角形的面积公式,考查化简、计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.
如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
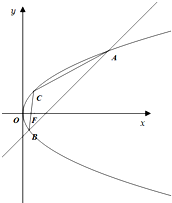 已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.
已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
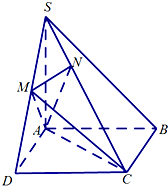 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,M为SD的中点,AN⊥SC,且交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AB,M为SD的中点,AN⊥SC,且交SC于点N. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:4 | B. | 2:3 | C. | 1:3 | D. | 1:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com