
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
分析 设F′为椭圆的左焦点,连接AF′,BF′,则四边形AFBF′是平行四边形,可得4=|AF|+|BF|=|AF′|+|BF|=2a.解得a=2,取M(0,b),由点M到直线l的距离$\frac{4}{5}$,得到b=1,由a,b,c的关系可得c,进而得到焦距2c.
解答 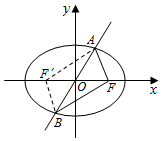 解:如图所示,
解:如图所示,
设F′为椭圆的左焦点,连接AF′,BF′,
则四边形AFBF′是平行四边形,
可得|AF|+|BF|=|AF|+|AF′|=2a=4,解得a=2.
取M(0,b),可得点M到直线l的距离$\frac{4}{5}$,
即有$\frac{4b}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{4}{5}$,解得b=1,
c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,
则焦距为2c=2$\sqrt{3}$.
故选:A.
点评 本题考查了椭圆的定义、标准方程及其性质、点到直线的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 生二胎 | 不生二胎 | 合计 | |
| 70后 | 30 | 15 | 45 |
| 80后 | 45 | 10 | 55 |
| 合计 | 75 | 25 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
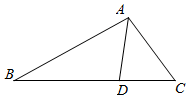 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com