
分析 (Ⅰ)由题意可得,2b=2,再由椭圆的离心率公式和a,b,c的关系,解得a=2,进而得到椭圆方程;
(Ⅱ)方法一、设P(x0,y0)(0<x0≤2),A(0,-1),B(0,1),求出直线PA,PB的方程,与直线x=4的交点M,N,可得MN的中点,圆的方程,令y=0,求得与x轴的交点坐标,运用弦长公式,结合${x_0}∈(\frac{8}{5},2]$.即可得到所求最大值;
方法二、设P(x0,y0)(0<x0≤2),A(0,-1),B(0,1),求出直线PA,PB的方程,与直线x=4的交点M,N,以MN为直径的圆与x轴相交,可得yMyN<0,求得${x_0}∈(\frac{8}{5},2]$,再由弦长公式,可得最大值.
解答 解:(Ⅰ)由题意可得,2b=2,即b=1,
$e=\frac{c}{a}=\frac{{\sqrt{3}}}{2}$,得$\frac{{{a^2}-1}}{a^2}=\frac{3}{4}$,
解得a2=4,
椭圆C的标准方程为$\frac{x^2}{4}+{y^2}=1$;
(Ⅱ)方法一、设P(x0,y0)(0<x0≤2),A(0,-1),B(0,1),
所以${k_{PA}}=\frac{{{y_0}+1}}{x_0}$,直线PA的方程为$y=\frac{{{y_0}+1}}{x_0}x-1$,
同理:直线PB的方程为$y=\frac{{{y_0}-1}}{x_0}x+1$,
直线PA与直线x=4的交点为$M(4,\frac{{4({y_0}+1)}}{x_0}-1)$,
直线PB与直线x=4的交点为$N(4,\frac{{4({y_0}-1)}}{x_0}+1)$,
线段MN的中点$(4,\frac{{4{y_0}}}{x_0})$,
所以圆的方程为${(x-4)^2}+{(y-\frac{{4{y_0}}}{x_0})^2}={(1-\frac{4}{x_0})^2}$,
令y=0,则${(x-4)^2}+\frac{16y_0^2}{x_0^2}={(1-\frac{x_0}{4})^2}$,
因为$\frac{x_0^2}{4}+y_0^2=1$,所以 $\frac{y_0^2-1}{x_0^2}=-\frac{1}{4}$,
所以${(x-4)^2}+\frac{8}{x_0}-5=0$,
设交点坐标(x1,0),(x2,0),可得x1=4+$\sqrt{5-\frac{8}{{x}_{0}}}$,x2=4-$\sqrt{5-\frac{8}{{x}_{0}}}$,
因为这个圆与x轴相交,该方程有两个不同的实数解,
所以 $5-\frac{8}{x_0}>0$,解得${x_0}∈(\frac{8}{5},2]$.
则$|{x_1}-{x_2}|=2\sqrt{5-\frac{8}{x_0}}$($\frac{8}{5}<{x_0}≤2$)
所以当x0=2时,该圆被x轴截得的弦长为最大值为2.
方法二:设P(x0,y0)(0<x0≤2),A(0,-1),B(0,1),
所以${k_{PA}}=\frac{{{y_0}+1}}{x_0}$,直线PA的方程为$y=\frac{{{y_0}+1}}{x_0}x-1$,
同理:直线PB的方程为$y=\frac{{{y_0}-1}}{x_0}x+1$,
直线PA与直线x=4的交点为$M(4,\frac{{4({y_0}+1)}}{x_0}-1)$,
直线PB与直线x=4的交点为$N(4,\frac{{4({y_0}-1)}}{x_0}+1)$,
若以MN为直径的圆与x轴相交,
则$[\frac{{4({y_0}+1)}}{x_0}-1]×$$[\frac{{4({y_0}-1)}}{x_0}+1]<0$,
即$\frac{16(y_0^2-1)}{x_0^2}-\frac{{4({y_0}-1)}}{x_0}+\frac{{4({y_0}+1)}}{x_0}-1<0$,
即$\frac{16(y_0^2-1)}{x_0^2}+\frac{8}{x_0}-1<0$.
因为$\frac{x_0^2}{4}+y_0^2=1$,所以$\frac{y_0^2-1}{x_0^2}=-\frac{1}{4}$,
代入得到$5-\frac{8}{x_0}>0$,解得${x_0}∈(\frac{8}{5},2]$.
该圆的直径为$|\frac{{4({y_0}+1)}}{x_0}-1-(\frac{{4({y_0}-1)}}{x_0}+1)|=|2-\frac{8}{x_0}|$,
圆心到x轴的距离为$\frac{1}{2}|\frac{{4({y_0}+1)}}{x_0}-1+(\frac{{4({y_0}-1)}}{x_0}+1)|=|\frac{{4{y_0}}}{x_0}|$,
该圆在x轴上截得的弦长为$2\sqrt{{{(1-\frac{4}{x_0})}^2}-{{(\frac{{4{y_0}}}{x_0})}^2}}=2\sqrt{5-\frac{8}{x_0}},(\frac{8}{5}<x≤2)$;
所以该圆被x轴截得的弦长为最大值为2.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和基本量的关系,考查直线和圆相交的弦长问题,注意运用圆的方程,以及直线和圆相交的条件,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{π}{3}$,$\frac{π}{6}$] | B. | [-$\frac{π}{4}$,$\frac{π}{4}$] | C. | [$\frac{π}{6}$,$\frac{2π}{3}$] | D. | [$\frac{π}{4}$,$\frac{3π}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.
如图,已知抛物线C:y2=4x,为其准线,过其对称轴上一点P(2,0)作直线l′与抛物线交于A(x1,y1)、B(x2,y2)两点,连结OA、OB并延长AO、BO分别交l于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
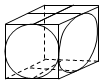 刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )
刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
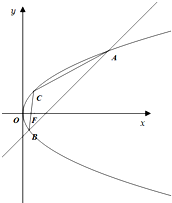 已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.
已知抛物线y2=4x,焦点为F,过点(2,0)且斜率为正数的直线交抛物线于A,B两点,且$\overrightarrow{FA}$•$\overrightarrow{FB}$=-11.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com