
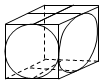
 刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )
刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 计算出V方盖差,V正,即可得出结论
解答 解:解:由题意,V方盖差=r3-$\frac{1}{8}$V牟=r3-$\frac{1}{8}$×$\frac{4}{π}$×$\frac{4}{3}$×π×r3=$\frac{1}{3}$r3,
所有棱长都为r的正四棱锥的体积为V正=$\frac{1}{3}$×$r×r×\sqrt{{r}^{2}-(\frac{\sqrt{2}r}{2})^{2}}$=$\frac{\sqrt{2}}{6}$r3,
∴$\frac{{V}_{方盖差}}{{V}_{正}}$=$\frac{\frac{1}{3}{r}^{3}}{\frac{\sqrt{2}{r}^{3}}{6}}$=$\sqrt{2}$,
故选:C.
点评 本题考查新定义,考查体积的计算,考查学生分析解决问题的能力,比较基础


科目:高中数学 来源: 题型:解答题
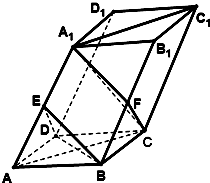 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的菱形,AA1=2$\sqrt{6}$,BD⊥BB1,∠BAD=60°,∠A1AC=45°,点E、F分别是线段AA1,BB1的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的菱形,AA1=2$\sqrt{6}$,BD⊥BB1,∠BAD=60°,∠A1AC=45°,点E、F分别是线段AA1,BB1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | {(-1,3)} | C. | {-1,3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.
如图,已知长方体ABCD-A1B1C1D1,AB=2,AA1=1,直线BD与平面AA1B1B所成的角为30°,AE垂直BD于E,F为A1B1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com