
分析 (Ⅰ)由题意可得b=1,2a=2$\sqrt{2}$c,结合a,b,c的关系,可得a,c,进而得到椭圆方程;
(Ⅱ)原点在线段AB为直径的圆外.求出AB的方程,代入椭圆方程,求得A,B的坐标,可得圆心和半径,求得O与圆心的距离,即可判断;
(Ⅲ)设直线AB的方程为y=k(x+1),代入椭圆方程x2+2y2=2,设A(x1,y1),B(x2,y2),运用韦达定理,再求y1y2=k2(x1+1)(x2+1),由点O在以线段AB为直径的圆内,可得∠AOB为钝角,即为$\overrightarrow{OA}$•$\overrightarrow{OB}$<0,即有x1x2+y1y2<0,代入解不等式即可得到所求k的范围.
解答 解:(Ⅰ)由题意可得b=1,2a=2$\sqrt{2}$c,
即有a=$\sqrt{2}$c,a2-c2=b2=1,
解得a=$\sqrt{2}$,c=1,
则椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(Ⅱ)原点在线段AB为直径的圆外.
理由:由左焦点F(-1,0),可得直线AB的方程为x=-1,
代入椭圆方程x2+2y2=2,可得y=±$\frac{\sqrt{2}}{2}$,
即有A(-1,$\frac{\sqrt{2}}{2}$),B(-1,-$\frac{\sqrt{2}}{2}$),
可得圆心为(-1,0),半径为$\frac{\sqrt{2}}{2}$,
由原点到圆心的距离为1,且1>$\frac{\sqrt{2}}{2}$,
则原点在线段AB为直径的圆外;
(Ⅲ)设直线AB的方程为y=k(x+1),
代入椭圆方程x2+2y2=2,可得(1+2k2)x2+4k2x+2k2-2=0,
设A(x1,y1),B(x2,y2),
可得x1+x2=-$\frac{4{k}^{2}}{1+2{k}^{2}}$,x1x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$,
y1y2=k2(x1+1)(x2+1)=k2(x1x2+x1+x2+1)
=k2($\frac{2{k}^{2}-2}{1+2{k}^{2}}$-$\frac{4{k}^{2}}{1+2{k}^{2}}$+1)=-$\frac{{k}^{2}}{1+2{k}^{2}}$,
由点O在以线段AB为直径的圆内,可得∠AOB为钝角,
即为$\overrightarrow{OA}$•$\overrightarrow{OB}$<0,即有x1x2+y1y2<0,
即$\frac{2{k}^{2}-2}{1+2{k}^{2}}$-$\frac{{k}^{2}}{1+2{k}^{2}}$<0,
解得-$\sqrt{2}$<k<$\sqrt{2}$.
则直线AB的斜率k的取值范围是(-$\sqrt{2}$,$\sqrt{2}$).
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质,考查点与圆的位置关系,注意运用点与圆心的距离和半径的关系,以及点与直径的端点的张角与向量的数量积的符号的关系,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
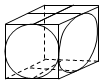 刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )
刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | 24π | C. | 36π | D. | 48π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{3}$ | C. | $\frac{{7\sqrt{6}}}{3}$ | D. | $2\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18π | B. | 19π | C. | 20π | D. | 21π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com