
分析 (1)求得f(x)的导数,由偶函数的定义,可得b=0,求得a=1,进而得到f(x)的解析式;
(2)求出g(x)的解析式,求得导数,分解因式,判断g(x)在[1,2]的单调性,可得最值,要满足题意,只需c≥|g(x1)-g(x2)|max,计算即可得到c的最小值;
(3)设切点为(x0,y0),求出函数y的导数,切线的斜率和方程,代入(2,m),可得m=-3x04+8x03+3x02-12x0,(*)设h(x)=-3x4+8x3+3x2-12x,求出h(x)的导数,单调区间,可得极值,由条件即可得到m的值.
解答 解:(1)函数f(x)=ax3+bx2-3x的导数为f′(x)=3ax2+2bx-3,
f′(x)是偶函数,可得f′(-x)=f′(x),
即3ax2+2bx-3=3ax2-2bx-3,解得b=0,
又f′(1)=0,即3a-3=0,解得a=1,
即有f(x)=x3-3x;
(2)g(x)=$\frac{1}{3}$f(x)-6lnx=$\frac{1}{3}$x3-x-6lnx,
g′(x)=x2-1-$\frac{6}{x}$=$\frac{{x}^{3}-x-6}{x}$=$\frac{{x}^{3}-8-(x-2)}{x}$=$\frac{(x-2)({x}^{2}+2x+3)}{x}$,
由x∈[1,2],g′(x)<0,g(x)在[1,2]递减,
可得g(x)max=g(1)=-$\frac{2}{3}$,g(x)min=g(2)=$\frac{2}{3}$-6ln2,
若要满足题意,只需c≥|g(x1)-g(x2)|max=g(1)-g(2)=-$\frac{4}{3}$+6ln2,
即cmin=-$\frac{4}{3}$+6ln2;
(3)y=xf(x)=x4-3x2,设切点为(x0,y0),y0=x04-3x02,
导数y′=4x3-6x,切线的斜率k=4x03-6x0,
切线的方程为y-(x04-3x02)=(4x03-6x0)(x-x0),
将(2,m)代入可得m-(x04-3x02)=(4x03-6x0)(2-x0)
m=-3x04+8x03+3x02-12x0,(*)
设h(x)=-3x4+8x3+3x2-12x,
可得h′(x)=-12x3+24x2+6x-12=-6(x-2)(2x2-1),
由h′(x)>0可得x<-$\frac{\sqrt{2}}{2}$或$\frac{\sqrt{2}}{2}$<x<2;
由h′(x)<0可得-$\frac{\sqrt{2}}{2}$<x<$\frac{\sqrt{2}}{2}$或x>2.
即有h(x)在(-∞,-$\frac{\sqrt{2}}{2}$),($\frac{\sqrt{2}}{2}$,2)递增;在(2,+∞),(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)递减.
可得h(x)在x=-$\frac{\sqrt{2}}{2}$处取得极大值$\frac{3}{4}$+4$\sqrt{2}$;在x=2处取得极大值为4;
在x=$\frac{\sqrt{2}}{2}$处取得极大值$\frac{3}{4}$-4$\sqrt{2}$.
可得m=4或$\frac{3}{4}$-4$\sqrt{2}$时,(*)有三解.
综上可得实数m的取值范围是{4,$\frac{3}{4}$-4$\sqrt{2}$}.
点评 本题考查导数的运用:求求切线的方程和单调区间、极值和最值,考查不等式恒成立问题的解法,注意转化为求函数的最值问题,考查构造函数法,运用导数求得极值,考查化简整理的运算能力,属于中档题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | y=ex | B. | y=sin2x | C. | y=-x3 | D. | y=log${\;}_{\frac{1}{2}}}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
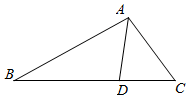 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=7,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 98 | B. | 99 | C. | 100 | D. | 101 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com