
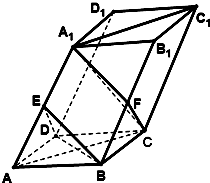
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的菱形,AA1=2$\sqrt{6}$,BD⊥BB1,∠BAD=60°,∠A1AC=45°,点E、F分别是线段AA1,BB1的中点.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD是边长为4的菱形,AA1=2$\sqrt{6}$,BD⊥BB1,∠BAD=60°,∠A1AC=45°,点E、F分别是线段AA1,BB1的中点.分析 (I)(方法一)连接EF,证明BE∥A1F,CF∥DE,即可证明平面BDE∥平面A1CF;
(方法二)设AC∩BD=O,连接EO,同方法一证明BE∥A1F,OE∥A1C,即可证明平面BDE∥平面A1CF;
(Ⅱ)(方法一)连接A1O,过点E作EP∥A1O,与AC交于P点,证明△AOA1为Rt△,A1O⊥AO,BD⊥A1O,BD∩AC=O,可得A1O⊥平面ABCD,利用等体积法求三棱锥B-ADE的体积;
(方法二)过点E作EP⊥AC交AC于点P,证明EP⊥平面ABCD,利用等体积法求三棱锥B-ADE的体积.
解答 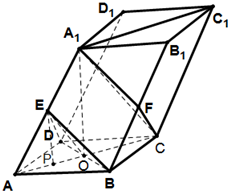 (I)证明:(方法一)连接EF,
(I)证明:(方法一)连接EF,
由已知可得:AA1$\underline{\underline∥}$BB1,∵点E、F分别是线段AA1,BB1的中点,
∴A1E$\underline{\underline∥}$BF,∴四边形BEA1F为平行四边形,
∴BE∥A1F,
同理:四边形CFED为平行四边形,∴CF∥DE,…(2分)
∵BE?平面BDE,DE?平面BDE,BE∩DE=E,CF?平面A1CF,A1F?平面A1CF,CF∩A1F=F,
∴平面A1FC∥平面BDE.…(4分)
(方法二)设AC∩BD=O,连接EO,
同方法一证明BE∥A1F,…(2分)
∵O、E分别为AC1,AA1的中点,∴OE∥A1C,
∵OE?平面BDE,BE?平面BDE,OE∩BE=ECF?平面A1CF,A1F?平面A1CF,CF∩A1F=F,
∴平面A1FC∥平面BDE.…(4分)
(Ⅱ)解:(方法一)连接A1O,过点E作EP∥A1O,与AC交于P点,
由已知可得:$BO=2,AO=2\sqrt{3},BD⊥AC$,
在△AA1O中,${({A_1}O)^2}={(A{A_1})^2}+{(AO)^2}-2A{A_1}•AO•cos{45°}$
=${(2\sqrt{6})^2}+{(2\sqrt{3})^2}-2×2\sqrt{6}×2\sqrt{3}×\frac{{\sqrt{2}}}{2}=12$,∴${A_1}O=2\sqrt{3}$,
∴△AOA1为Rt△,A1O⊥AO,…(6分)
又∵BD⊥BB1,AA1∥BB1,∴BD⊥AA1,AA1∩AC=A,
∴BD⊥平面ACC1A1,A1O?平面ACC1A1
∴BD⊥A1O,BD∩AC=O,∴A1O⊥平面ABCD,…(9分)
∵EP∥A1O,且点E为AA1的中点,∴$EP⊥平面ABCD,且EP=\sqrt{3}$,
∴${V_{E-ABD}}=\frac{1}{3}{S_{△ABD}}•EP=\frac{1}{3}×\frac{1}{2}×4×2\sqrt{3}×\sqrt{3}=4$,…(11分)
∴VB-ADE=VE-ABD=4.∴三棱锥B-ADE的体积为4.…(12分)
(方法二)∵ABCD为菱形,∴BD⊥AC,
∵BB1∥AA1,BD⊥BB1,∴BD⊥AA1,
∵AC∩AA1=A,∴BD⊥平面AA1C1C
又∵BD?平面ABCD,∴平面ABCD⊥平面AA1C1C
∵平面AA1C1C∩平面ABCD=AC,过点E作EP⊥AC交AC于点P,∵EP?平面AA1C1C,∴EP⊥平面ABCD,$在Rt△AEP中,∠A{A_1}C=4{5°},AE=\frac{1}{2}A{A_1}$,∴$EP=\sqrt{3}$,
∴${V_{B-ADE}}={V_{E-ABD}}=\frac{1}{3}×\frac{1}{2}×4×4×\sqrt{3}•sin{60°}=4$.…(12分)
点评 本题考查直线与平面平行的判定,考查平面与平面平行的判断及棱锥的体积,考查推理分析与运算能力,考查等价转化思想与数形结合思想的综合运用,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z) | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$](k∈Z) | ||
| C. | [kπ-$\frac{π}{6}$,kπ+$\frac{5π}{6}$](k∈Z) | D. | [kπ+$\frac{5π}{6}$,kπ+$\frac{11π}{6}$](k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收到的手机红包金额t(单位:元) | t≤100 | 100<t≤1000 | t>1000 |
| 人数(单位:人) | 150 | 100 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )
刘徽在他的《九章算术注》中提出一个独特的方法来计算球体的体积:他不直接给出球体的体积,而是先计算另一个叫“牟合方盖”的立体的体积.刘徽通过计算,“牟合方盖”的体积与球的体积之比应为$\frac{4}{π}$.后人导出了“牟合方盖”的$\frac{1}{8}$体积计算公式,即$\frac{1}{8}$V牟=r3-V方盖差,r为球的半径,也即正方形的棱长均为2r,为从而计算出V球=$\frac{4}{3}$πr3.记所有棱长都为r的正四棱锥的体积为V正,棱长为2r的正方形的方盖差为V方盖差,则$\frac{{V}_{方盖差}}{{V}_{正}}$=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com