
| �յ����ֻ�������t����λ��Ԫ�� | t��100 | 100��t��1000 | t��1000 |
| ��������λ���ˣ� | 150 | 100 | 50 |
���� ����Ƶ����Ϊ���ʣ����ij���յ����ֻ�������t��100��100��t��1000��t��1000�ĸ��ʣ��ɴ����û����¼��ӷ���ʽ�������ѡ1�ˣ��յ����ֻ��������100Ԫ�ĸ��ʣ�
�����衰��4��������ѡȡ1�ˣ�������1���յ����ֻ��������100Ԫ��Ϊ�¼�A���ɴ�����n�ζ����ظ�����������¼�������1���յ����ֻ��������100Ԫ�ĸ��ʣ�
����i���ɷֲ�����������������Ϊ2�������У��յ��ֻ�������t��100��100��t��1000��t��1000�������ֱ�Ϊ3��8��1���ɴ��������ȡ��12���У��յ��ֻ��������100Ԫ��������
��ii��X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��м���ѧ������
��� �⣺����Ƶ����Ϊ���ʣ�ij���յ����ֻ�������t��100��100��t��1000��t��1000�ĸ��ʷֱ�Ϊ��
${p}_{1}=\frac{150}{600}$=$\frac{1}{4}$��p2=$\frac{400}{600}$=$\frac{2}{3}$��p3=$\frac{50}{600}$=$\frac{1}{12}$��
����ѡ1�ˣ��յ����ֻ��������100Ԫ�ĸ���Ϊ��
p=p2+p3=$\frac{2}{3}+\frac{1}{12}$=$\frac{3}{4}$��
�����衰��4��������ѡȡ1�ˣ�������1���յ����ֻ��������100Ԫ��Ϊ�¼�A��
��P��A��=${C}_{4}^{0}��\frac{1}{4}��^{4}+{C}_{4}^{1}��\frac{1}{4}��^{3}��\frac{3}{4}��$=$\frac{13}{256}$��
�����ɷֲ������֪��
��������Ϊ2�������У��յ��ֻ�������t��100��100��t��1000��t��1000�������ֱ�Ϊ3��8��1��
��i����ȡ��12���У��յ��ֻ��������100Ԫ������Ϊ8+1=9��
��ii��X�Ŀ���ȡֵΪ0��1��2��3��
P��X=0��=$\frac{{C}_{3}^{0}}{{C}_{12}^{3}}$=$\frac{1}{220}$��
P��X=1��=$\frac{{C}_{9}^{1}{C}_{3}^{2}}{{C}_{12}^{3}}$=$\frac{27}{220}$��
P��X=2��=$\frac{{C}_{9}^{2}{C}_{3}^{1}}{{C}_{12}^{3}}$=$\frac{27}{55}$��
P��X=3��=$\frac{{C}_{9}^{3}}{{C}_{12}^{3}}$=$\frac{21}{55}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | ||
| P | $\frac{1}{220}$ | $\frac{27}{220}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��м���ѧ�����������е��⣬����ʱҪ�������⣬ע���������֪ʶ�ĺ������ã�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $2\sqrt{3}$ | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ������ABC-A1B1C1�У�AC=1��BC=2��AC��BC��D��E��F�ֱ�Ϊ��AA1��A1B1��AC���е㣮
��ͼ����ֱ������ABC-A1B1C1�У�AC=1��BC=2��AC��BC��D��E��F�ֱ�Ϊ��AA1��A1B1��AC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
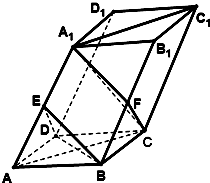 ��ͼ����������ABCD-A1B1C1D1�У�����ABCD�DZ߳�Ϊ4�����Σ�AA1=2$\sqrt{6}$��BD��BB1����BAD=60�㣬��A1AC=45�㣬��E��F�ֱ����߶�AA1��BB1���е㣮
��ͼ����������ABCD-A1B1C1D1�У�����ABCD�DZ߳�Ϊ4�����Σ�AA1=2$\sqrt{6}$��BD��BB1����BAD=60�㣬��A1AC=45�㣬��E��F�ֱ����߶�AA1��BB1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1����2�� | B�� | ��1��2�� | C�� | ��1��-2 �� | D�� | ��1����1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
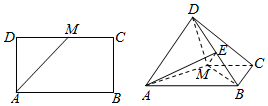
 ��ͼ����֪������ABCD-A1B1C1D1��AB=2��AA1=1��ֱ��BD��ƽ��AA1B1B���ɵĽ�Ϊ30�㣬AE��ֱBD��E��FΪA1B1���е㣮
��ͼ����֪������ABCD-A1B1C1D1��AB=2��AA1=1��ֱ��BD��ƽ��AA1B1B���ɵĽ�Ϊ30�㣬AE��ֱBD��E��FΪA1B1���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com