
| A. | (1,±2) | B. | (1,2) | C. | (1,-2 ) | D. | (1,±1) |
分析 根据抛物线解析式确定出焦点F坐标,设设A($\frac{{{y}_{0}}^{2}}{4}$,y0),表示出$\overrightarrow{OA}$与$\overrightarrow{AF}$,代入已知等式,利用平面整理的数量积运算法则计算,确定出y0的值,即可求出A坐标.
解答 解:依题意得F(1,0),
设A($\frac{{{y}_{0}}^{2}}{4}$,y0),则$\overrightarrow{OA}$=($\frac{{{y}_{0}}^{2}}{4}$,y0),$\overrightarrow{AF}$=(1-$\frac{{{y}_{0}}^{2}}{4}$,-y0),
∵$\overrightarrow{OA}$•$\overrightarrow{AF}$=-4,
∴$\frac{{{y}_{0}}^{2}}{4}$(1-$\frac{{{y}_{0}}^{2}}{4}$)-y02=-4,
解得:y0=±2,
则点A的坐标为(1,±2).
故选:A.
点评 此题考查了抛物线的简单性质,以及平面向量的数量积运算,熟练掌握抛物线的简单性质是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{1}{35}$ | C. | $\frac{8}{35}$ | D. | $\frac{7}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 收到的手机红包金额t(单位:元) | t≤100 | 100<t≤1000 | t>1000 |
| 人数(单位:人) | 150 | 100 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
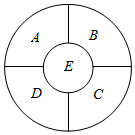 将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:
将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10π | B. | 24π | C. | 36π | D. | 48π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com