
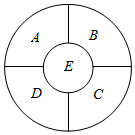
 将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:
将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:分析 根据题意,分析可得重复的数字只能是1且只能填在BD或AC处,有2种情况;对于中间位置,分析可得只能放0或4,有2种情况;最后将剩下的2个数字全排列放入剩下的2个位置,计算可得其情况数目,最后由分步计数原理计算可得答案.
解答 解:根据题意,四个数字中只允许一个数字重复出现,且各位置数字之和为偶数,则重复的数字只能是1,
又由相同数字不可相邻,则1只能填在BD或AC处,有2种情况;
对于中间位置,要求其可被其余四个数字之和整除,则中间位置只能放0或4,有2种情况,
对于剩下的位置,将剩下的2个数字全排列即可,有A22=2种情况,
故有2×2×2=8种情况;
答:不同的填写方法有8种.
点评 本题考查排列、组合的实际应用,关键是分析题目中的要求,分析得到各个位置、各个数字的要求.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AC=1,BC=2,AC⊥BC,D,E,F分别为棱AA1,A1B1,AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=1,BC=2,AC⊥BC,D,E,F分别为棱AA1,A1B1,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,±2) | B. | (1,2) | C. | (1,-2 ) | D. | (1,±1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,4] | B. | (-3,4) | C. | (0,1] | D. | (-1,4] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com