
分析 利用函数的奇偶性、函数的图象的对称性,数形结合可得函数的周期性以及单调性,从而得出结论.
解答 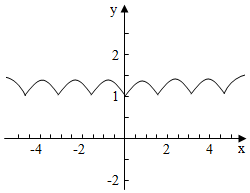 解:由于函数f(x)=|sinx|+|cosx|为偶函数,故①正确;
解:由于函数f(x)=|sinx|+|cosx|为偶函数,故①正确;
画出函数位于y轴右侧的图象,如图所示,
再根据函数f(x)的图象关于y轴对称,
可得函数f(x)在R上的图象,如图所示:
数形结合可得函数的最小正周期为$\frac{π}{2}$,故②不正确,
③正确;
由于在$[0,\frac{π}{2}]$上,$f(x)=sinx+cosx=\sqrt{2}sin(x+\frac{π}{4})$,
结合它的最小正周期为$\frac{π}{2}$,
故该函数单调递增区间为[$\frac{kπ}{2}$,$\frac{π}{4}$+$\frac{kπ}{2}$],k∈Z,
故④正确,
故答案为:①③④.
点评 本题主要考查正弦函数的图象和性质,体现了数形结合的数学思想,属于中档题.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
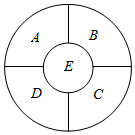 将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:
将2,0,1,4四个数字填入图中位置,只允许一个数字重复出现,并且满足以下要求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 调查的方式是普查 | B. | 本地区约有15%的成年人吸烟 | ||
| C. | 样本是15个吸烟的成年人 | D. | 本地区只有85个成年人不吸烟 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com