练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．三棱锥P-ABC中，AB=BC=$\sqrt{2}$，AC=2，PC⊥平面ABC，PC=2，则该三棱锥的外接球表面积为8π．

    分析 根据已知条件得出线面的垂直，构造长方体，得出外接球的半径即可．

    解答 解：∵三棱锥P-ABC中，AB=BC=$\sqrt{2}$，AC=2，PC⊥平面ABC，PC=2，
    ∴运用勾股定理盘AB⊥BC
    构造长方体如图：长$\sqrt{2}$，宽$\sqrt{2}$高2，
    体对角线为：$\sqrt{2+2+4}$=2$\sqrt{2}$，
    ∴该三棱锥的外接球半径为$\sqrt{2}$，表面积为：4π×2=8π，

    故答案为：8π．

    点评 本题综合考查了空间几何体的性质，运用构造法解决外接球的问题，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=|sinx|+|cosx|，现有如下几个命题：
    ①该函数为偶函数；
    ②该函数最小正周期为π；
    ③该函数值域为[1，$\sqrt{2}$]；
    ④该函数单调递增区间为[$\frac{kπ}{2}$，$\frac{π}{4}$+$\frac{kπ}{2}$]，k∈Z．
    其中正确命题为①③④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．函数f（x）的定义域为D，若满足：①f（x）在D内是单调函数；　②若存在[a，b]⊆D，使得f（x）在[a，b]上的值域为[2a，2b]，则称函数f（x）为“成功函数”．若函数f（x）=logc（c4x+3t）（c＞0，c≠1）是“成功函数”，则t的取值范围为（0，$\frac{1}{12}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．在△ABC中，∠ACB=90°，点P是平面ABC外一点，且PC=24，若点P到直线AC、BC的距离都等于$6\sqrt{10}$，则PC与平面ABC所成角的大小为30°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知点A（-2，0），P是⊙O：x2+y2=4上任意一点，P在x轴上的射影为Q，$\overrightarrow{QP}$=2$\overrightarrow{QG}$，动点G的轨迹为C，直线y=kx（k≠0）与轨迹交于E，F两点，直线AE，AF分别与y轴交于点M，N．
    （1）求轨迹C的方程；
    （2）以MN为直径的圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．在△ABC中，已知∠A=135°，∠B=15°，c=1，则a=$\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某校在高三抽取了500名学生，记录了他们选修A、B、C三门课的选修情况，如表：
     科目
    学生人数    		 A B C
     120 是 否 是
     60 否 否 是
     70 是 是 否
     50 是 是 是
     150 否 是 是
     50 是 否 否
    （Ⅰ）试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率．
    （Ⅱ）若该高三某学生已选修A，则该学生同时选修B、C中哪门的可能性大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知集合A={（x，y）|y=x2}，B={（x，y）|y=$\sqrt{x}$}，则A∩B=（　　）
    A．{0，1}B．{0}C．{（1，1）}D．{（0，0），（1，1）}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

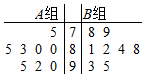    13．某高三文科班有A，B两个学习小组，每组8人，在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示：
    （1）这两组学生历史成绩的中位数和平均数分别是多少？
    （2）历史老师想要在这两个学习小组中选择一个小组进行奖励，请问选择哪个小组比较好，只说明结论，不用说明理由；
    （3）若成绩在90分以上（包括90分）的同学视为优秀，则从这两组历史成绩优秀的学生中抽取2人，求至少有一人来自B学习小组的概率．

    查看答案和解析>>

    同步练习册答案