
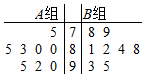
 某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:
某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:分析 (1)由茎叶图能求出A、B两组学生历史成绩的中位数和平均分.
(2)因为两组学生的平均分相同,但是B组学生的成绩比A组学生的成绩更集中,从而选择B组学生奖励.
(3)由题可知A组历史成绩优秀的学生有3人,B组历史成绩优秀的学生有2人,由此利用列举法能求出至少有一人来自B学习小组的概率.
解答 解:(1)A组学生历史成绩的中位数为84,B组学生历史成绩的中位数为83
A组学生历史成绩的平均分为$\frac{75+80+80+83+85+90+92+95}{8}=85$
B组学生历史成绩的平均分为$\frac{78+79+81+82+84+88+93+95}{8}$=85
(2)选择B组学生奖励,因为两组学生的平均分相同,但是B组学生的成绩比A组学生的成绩更集中.
(3)由题可知A组历史成绩优秀的学生有3人,分别设为a1,a2,a3,
B组历史成绩优秀的学生有2人,分别设为b1,b2,因此两个学习小组历史成绩优秀的学生共有5人.
从这5人中抽取2人共包含10种情况,分别为:
(a1,a2),(a1,a3),(a1,b1),(a1,b2),(a2,a3),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2),
记“至少有一人来自B学习小组”为事件A,则事件A共包含7种情况,分别为:
(a1,b1),(a1,b2),(a2,b1),(a3,b1),(a3,b2),(b1,b2),
因此P(A)=$\frac{7}{10}$ 所以至少有一人来自B学习小组的概率为$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意茎叶图性质、列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
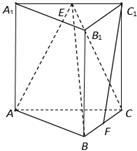 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:在三棱柱ABC-A1B1C1中,底面是边长为2$\sqrt{3}$的正三角形,点A1在底面ABC上的射影O恰是BC中点.
如图:在三棱柱ABC-A1B1C1中,底面是边长为2$\sqrt{3}$的正三角形,点A1在底面ABC上的射影O恰是BC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com