
 如图:在三棱柱ABC-A1B1C1中,底面是边长为2$\sqrt{3}$的正三角形,点A1在底面ABC上的射影O恰是BC中点.
如图:在三棱柱ABC-A1B1C1中,底面是边长为2$\sqrt{3}$的正三角形,点A1在底面ABC上的射影O恰是BC中点.分析 (I)由A1O⊥平面ABC得A1O⊥BC,由三线合一得出AO⊥BC,故而BC⊥平面A1OA,于是AA1⊥BC;
(II)根据∠A1AO=45°得出棱柱的高A1O,则V${\;}_{A-BC{C}_{1}{B}_{1}}$=V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{2}{3}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$.
(III)过D作DE⊥AC于E,过A1作A1F⊥AC于F,连结BE,OF.通过证明AC⊥平面A1OF确定F点为AC的四等分点,通过证明AC⊥平面BDE确定E为AC的中点,于是$\frac{{A}_{1}D}{DA}=\frac{EF}{AE}$.
解答 证明:(I)连结AO,
∵A1O⊥平面ABC,BC?平面ABC,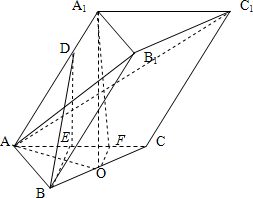
∴A1O⊥BC,
∵△ABC是正三角形,O是BC的中点,
∴AO⊥BC,
又AO?平面A1AO,A1O?平面A1AO,AO∩A1O=O,
∴BC⊥平面A1AO,∵AA1?平面A1AO,
∴BC⊥A1A.
(II)∵A1O⊥平面ABC,
∴∠A1AO为侧棱A1A与底面ABC所成的角,
∴∠A1AO=45°,
∵等边三角形ABC的边长为2$\sqrt{3}$,
∴AO=3,∴A1O=3.
∴V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$=S△ABC•A1O=$\frac{\sqrt{3}}{4}×(2\sqrt{3})^{2}×3$=9$\sqrt{3}$.
V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}$V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$=3$\sqrt{3}$.
∴V${\;}_{A-BC{C}_{1}{B}_{1}}$=V${\;}_{棱柱ABC-{A}_{1}{B}_{1}{C}_{1}}$-V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=6$\sqrt{3}$.
(III)$\frac{{A}_{1}D}{DA}=2$时,BD⊥A1C1,理由如下:
过D作DE⊥AC于E,过A1作A1F⊥AC于F,连结BE,OF.
∵A1O⊥平面ABC,AC?平面ABC,
∴A1O⊥AC,又A1F⊥AC,AF?平面A1OF,A1O?平面A1OF,A1O∩A1F=A1,
∴AC⊥平面A1OF,∵OF?平面A1OF,
∴AC⊥OF,
∵△ABC是等边三角形,O是BC的中点,
∴F为线段AC的靠近C点的四等分点,即AF=$\frac{3}{4}AC$=$\frac{3\sqrt{3}}{2}$.
∵BD⊥A1C1,AC∥A1C1,∴AC⊥BD.
又AC⊥DE,DE?平面BDE,BD?平面BDE,BD∩DE=D,
∴AC⊥平面BDE,∵BD?平面BDE,
∴AC⊥BE,
∵△ABC是等边三角形,∴E为AC的中点.即AE=$\frac{1}{2}AC$=$\sqrt{3}$.
∵DE⊥AC,A1F⊥AC,DE?平面AA1C1C,A1F?平面AA1C1C,
∴DE∥A1F,
∴$\frac{{A}_{1}D}{DA}=\frac{EF}{AE}$=$\frac{1}{2}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
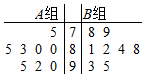 某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:
某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 种植地编号 | A1 | A2 | A3 | A4 | A5 |
| (x,y,z) | (0,1,0) | (1,2,1) | (2,1,1) | (2,2,2) | (0,1,1) |
| 种植地编号 | A6 | A7 | A8 | A9 | A10 |
| (x,y,z) | (1,1,2) | (2,1,2) | (2,0,1) | (2,2,1) | (0,2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
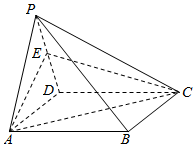 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是边长为2的正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是边长为2的正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
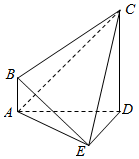 如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,DE=3.
如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,DE=3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | (0,e) | C. | ($\frac{1}{e}$,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com