
分析 (1)利用正弦定理化简表达式,求角B;个两角和与差的三角函数化简求解即可.
(2)利用余弦定理求边长b的最小值.推出b的表达式,利用基本不等式求解即可.
解答 解:(1)在△ABC中,由已知$\frac{cosC}{cosB}=\frac{2sinA-sinC}{sinB}$,
即cosCsinB=(2sinA-sinC)cosB,
sin(B+C)=2sinAcosB,sinA=2sinAcosB,…4分
△ABC 中,sinA≠0,
故$cosB=\frac{1}{2},B=\frac{π}{3}$. …6分.
(2)a+c=2,
由(1)$B=\frac{π}{3}$,因此b2=a2+c2-2accosB=a2+c2-ac …9分
由已知b2=(a+c)2-3ac=4-3ac …10分
$≥4-3{({\frac{a+c}{2}})^2}=4-3=1$ …11分
故b 的最小值为1.…12分
点评 本题考查正弦定理以及余弦定理的应用,两角和与差的三角函数,考查转化思想以及计算能力.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
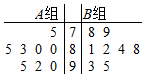 某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:
某高三文科班有A,B两个学习小组,每组8人,在刚刚进行的双基考试中这两组学生历史考试的成绩如图茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,3) | B. | [0,3) | C. | (-2,3) | D. | [-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
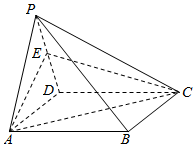 如图,四棱锥P-ABCD的底面是矩形,侧面PAD是边长为2的正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.
如图,四棱锥P-ABCD的底面是矩形,侧面PAD是边长为2的正三角形,且侧面PAD⊥底面ABCD,E为侧棱PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com