
分析 (1)当n=5时,集合A={1,2,3,4,5},由X⊆A,且2≤Card(X)≤3,则满足条件的X共有:${∁}_{5}^{2}+{∁}_{5}^{3}$=20个.
(2)对所有的X进行配对:①当Card(X)=2时,令X={x1,x2},X′={n+1-xi|xi∈X},必有X′⊆A,可得:${a_X}+{a_{X^/}}=2n+2$,如果X=X′则aX=n+1.②同理,当Card(X)=k(2<k≤n-2)时,也有上述结论.
解答 解:(1)当n=5时,集合A={1,2,3,4,5},∵X⊆A,且2≤Card(X)≤3,∴X={1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5},{1,2,3},{1,2,4},},{1,2,5},{1,3,4},},{1,3,5},{1,4,5},{2,3,4},{2,3,5},},{2,4,5},{3,4,5}.
因此共有${∁}_{5}^{2}+{∁}_{5}^{3}$=20个.
(2)对所有的X进行配对:
①当Card(X)=2时,
令X={x1,x2},X′={n+1-xi|xi∈X},必有X′⊆A,不妨设x1<x2,则aX=x1+x2,${a_{X^/}}=n+1-{x_1}+n+1-{x_2}=2n+2-({x_1}+{x_2})$.如果X≠X′,则有${a_X}+{a_{X^/}}=2n+2$,如果X=X′则aX=n+1.
②同理,当Card(X)=k(2<k≤n-2)时,
令X={x1,x2,…xk},X′={n+1-x&i|xi∈X}必有X′⊆A,不妨设x1<x2<…<xk,则aX=x1+xk,${a_{X^/}}=2n+2-({x_1}+{x_k})$.如果X≠X′,则${a_X}+{a_{X^/}}=2n+2$,如果X=X′则aX=n+1.
∴在每一组元素个数相同的子集中,aX的平均值为n+1.
综上,所有aX的算术平均值为n+1.
故答案分别为:20;n+1.
点评 本题考查了集合的运算性质、分类讨论方法,考查了分析问题与解决问题的能力、转化能力、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
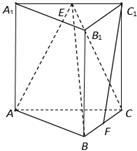 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
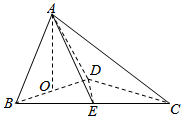 如图,四面体ABCD中,O、E分别 BD、BC的中点,AB=AD=$\sqrt{2}$,CA=CB=CD=BD=2.
如图,四面体ABCD中,O、E分别 BD、BC的中点,AB=AD=$\sqrt{2}$,CA=CB=CD=BD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com