
分析 (I)讨论当n=2k-1(k∈N*),当n=2k(k∈N*),化简等式,可得数列{an}的奇数项为首项为a1=1,公差为-2的等差数列;偶数项为首项a2=3,公比为3的等比数列.运用等差数列和等比数列的通项公式即可得到所求数列的通项,注意运用分段形式;
(Ⅱ)化简bn,当n=2k时,可得bn=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+2}$),再由数列的求和方法:分组求和,结合等差数列的求和公式和裂项相消求和,化简整理即可得到所求和.
解答 解:(I)当n=2k-1(k∈N*),a2k+1=(2+cos(2k-1)π)(a2k-1+1)-3,
即为a2k+1=a2k-1-2;
当n=2k(k∈N*),a2k+2=(2+cos(2kπ))(a2k+1)-3,
即为a2k+2=3a2k.
则数列{an}的奇数项为首项为a1=1,公差为-2的等差数列;
偶数项为首项a2=3,公比为3的等比数列.
即有a2k=a2•3k-1=3k;a2k-1=a1+(k-1)•(-2)=3-2k,
可得an=$\left\{\begin{array}{l}{{3}^{\frac{n}{2},}n=2k,k∈{N}^{*}}\\{2-n,n=2k-1,k∈{N}^{*}}\end{array}\right.$;
(Ⅱ)bn=$\left\{\begin{array}{l}{\frac{lo{g}_{3}{a}_{n}}{{n}^{2}(n+2)}=\frac{1}{2n(n+2)}=\frac{1}{4}(\frac{1}{n}-\frac{1}{n+2}),n=2k,K∈{N}^{*}}\\{2-n,n=2k-1,k∈{N}^{*}}\end{array}\right.$,
则T2n=(b1+b3+b5+…+b2n-1)+(b2+b4+b6+…+b2n)
=$\frac{n({b}_{1}+{b}_{2n-1})}{2}$+$\frac{1}{4}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{8}$+…+$\frac{1}{2n}$-$\frac{1}{2n+2}$)
=$\frac{n(1+3-2n)}{2}$+$\frac{1}{4}$($\frac{1}{2}$-$\frac{1}{2n+2}$)
=2n-n2+$\frac{n}{8n+8}$.
点评 本题考查数列的通项的求法,注意运用分类讨论思想方法,运用等差数列和等比数列的通项公式,考查数列的求和方法:注意运用分组求和,结合等差数列的求和公式和裂项相消求和,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>4或x<0} | B. | {x|1<x<4} | C. | {x|1<x≤4} | D. | {x|1≤x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|-2<x<2} | C. | {x|-2<x<0} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,AC=1,BC=2,AC⊥BC,D,E,F分别为棱AA1,A1B1,AC的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=1,BC=2,AC⊥BC,D,E,F分别为棱AA1,A1B1,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
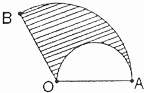 如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{5}{8π}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{8π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com