
分析 (1)先把(x+1)n化为[(x-1)+2]n,使用二项式定理计算;
(2)利用二项式定理求出an,代入计算化简再逆用二项式定理得出答案;
(3)求出bn,使用数学归纳法证明.
解答 解:(1)∵(x+1)n=[(x-1)+2]n=a0+a1(x-1)+a2(x-1)2+a3(x-1)3+…+an(x-1)n.
∴a0=${C}_{n}^{n}$•2n,
∴当n=5时,a0=${C}_{5}^{5}$•25=32.
(2)由(1)可知a1=${C}_{n}^{n-1}•{2}^{n-1}$,a2=${C}_{n}^{n-2}•{2}^{n-2}$,a3=${C}_{n}^{n-3}•{2}^{n-3}$,…an=${C}_{n}^{0}•{2}^{0}$.
∴$\frac{1}{n}$a1=2n-1=${C}_{n-1}^{0}•{2}^{n-1}$,$\frac{2}{n}$a2=(n-1)•2n-2=${C}_{n-1}^{1}•{2}^{n-2}$,…,$\frac{n-1}{n}$an-1=(n-1)•2=${C}_{n-1}^{n-2}•2$,$\frac{n}{n}$an=1=${C}_{n-1}^{n-1}•{2}^{0}$.
∴$\frac{1}{n}$a1+$\frac{2}{n}$a2+…+$\frac{n-1}{n}$an-1+$\frac{n}{n}$an=${C}_{n-1}^{0}•{2}^{n-1}$+${C}_{n-1}^{1}•{2}^{n-2}$+…+${C}_{n-1}^{n-1}•{2}^{0}$=(2+1)n-1=3n-1.
(3))由(1)可知a2=${C}_{n}^{n-2}$•2n-2=Cn2•2n-2=n(n-1)•2n-3.
∴bn=$\frac{{a}_{2}}{{2}^{n-3}}$=n(n-1)(n≥2).
①当n=2时.左边=T2=b2=2,右边=$\frac{2×3×1}{3}=2$,
∴左边=右边,等式成立.
②假设当n=k(k≥2,k∈N*)时,等式成立,即Tk=$\frac{k(k+1)(k-1)}{3}$,
则当n=k+1时,Tk+1=Tk+bk+1=$\frac{k(k+1)(k-1)}{3}$+(k+1)k=(k+1)k($\frac{k-1}{3}+1$)=$\frac{(k+1)(k+2)k}{3}$=$\frac{(k+1)(k+1+1)(k+1-1)}{3}$.
∴左边=右边,等式成立.
故当n=k+1时,等式成立.
综上①②,当n≥2时,Tn=$\frac{n(n+1)(n-1)}{3}$.
点评 本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、二项式定理的应用,考查利用数学归纳法证明恒等式,属于中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{16}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<0} | B. | {x|-2<x<2} | C. | {x|-2<x<0} | D. | {x|x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
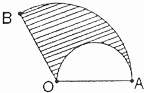 如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )
如图,在圆心角为120°的扇形OAB中,以OA为直径作一个半圆,若在扇形OAB内随机取一点,则此点取自阴影部分的概率是( )| A. | $\frac{5}{8π}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{8π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1,0,1,2} | B. | {-2,-1,0,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B?C | B. | A?B=C | C. | A?B?C | D. | B?C=A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2$\sqrt{3}$-2 | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com