Question

11．设点P是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）与圆x²+y²=a²+b²在第一象限内的交点，F₁，F₂分别是双曲线的左右焦点且|PF₁|=3|PF₂|，则双曲线的离心率为$\frac{\sqrt{10}}{2}$．

Answer 1

分析 由题意画出图形，可知PF₁⊥PF₂，由已知结合双曲线的定义求得|PF₁|，|PF₂|，再由勾股定理得答案．

解答 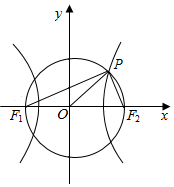解：如图，
∵圆x²+y²=a²+b² =c²，
∴F₁F₂为圆的直径，则PF₁⊥PF₂，
由$\left\{\begin{array}{l}{|P{F}_{1}|-|P{F}_{2}|=2a}\\{|P{F}_{1}|=3|P{F}_{2}|}\end{array}\right.$，解得|PF₁|=3a，|PF₂|=a，
∴$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}=9{a}^{2}+{a}^{2}=4{c}^{2}$，
即$\frac{{c}^{2}}{{a}^{2}}=\frac{10}{4}$，得e=$\frac{c}{a}=\frac{\sqrt{10}}{2}$．
故答案为：$\frac{\sqrt{10}}{2}$．

点评 本题考查双曲线的简单性质，考查了双曲线定义的应用，考查数形结合的解题思想方法，是中档题．