
【题目】设函数![]() 在
在![]() 上有意义,实数
上有意义,实数![]() 和
和![]() 满足
满足![]() ,若
,若![]() 在区间
在区间![]() 上不存在最小值,则称
上不存在最小值,则称![]() 在
在![]() 上具有性质
上具有性质![]() .
.
(1)当![]() ,且
,且![]() 在区间
在区间![]() 上具有性质
上具有性质![]() 时,求常数
时,求常数![]() 的取值范围;
的取值范围;
(2)已知![]() ,且当
,且当![]() ,
,![]() ,判断
,判断![]() 在区间
在区间![]() 上是否具有性质
上是否具有性质![]() ,请说明理由:
,请说明理由:
(3)若对于满足![]() 的任意实数
的任意实数![]() 和
和![]() ,
,![]() 在
在![]() 上具有性质
上具有性质![]() 时,且对任意
时,且对任意![]() ,当
,当![]() 时有:
时有:![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
【答案】(1)![]() ;(2)具有性质
;(2)具有性质![]() ;(3)略.
;(3)略.
【解析】
(1)分别讨论![]() 与1和2的关系,即可得出
与1和2的关系,即可得出![]() 是否存在最小值,从而求出
是否存在最小值,从而求出![]() 的取值范围;
的取值范围;
(2)由题目条件可得出![]() 在区间
在区间![]() ,
,![]() 上如果有最小值,则最小值必在区间
上如果有最小值,则最小值必在区间![]() ,
,![]() 上取到,又
上取到,又![]() 在区间
在区间![]() ,
,![]() 上不存在最小值,所以
上不存在最小值,所以![]() 在区间
在区间![]() ,
,![]() 上具有性质
上具有性质![]() ;
;
(3)首先证明对于任意![]() ,
,![]() ;其次证明当
;其次证明当![]() 且
且![]() 时,
时,![]() ;当
;当![]() 且
且![]() 时,
时,![]() ;最后证明:当
;最后证明:当![]() 时,
时,![]() .
.
解:(1)当![]() 时,
时,![]() 在
在![]() ,
,![]() 上存在最小值
上存在最小值![]() ;
;
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上存在最小值
上存在最小值![]() (2);
(2);
当![]() 时,
时,![]() 在
在![]() ,
,![]() 上单调递增,所以不存在最小值.
上单调递增,所以不存在最小值.
所以![]() .
.
(2)因为![]() 时,
时,![]() ,
,
所以![]() 在区间
在区间![]() ,
,![]() 上如果有最小值,则最小值必在区间
上如果有最小值,则最小值必在区间![]() ,
,![]() 上取到
上取到
另一方面,![]() 在区间
在区间![]() ,
,![]() 上不存在最小值,
上不存在最小值,
所以![]() 在区间
在区间![]() ,
,![]() 上具有性质
上具有性质![]() .
.
(3)①首先证明对于任意![]() ,
,![]() .
.
当![]() 时,由
时,由![]()
可知![]() 介于
介于![]() 和
和![]() 之间.若
之间.若![]() ,
,
则![]() 在区间
在区间![]() ,
,![]() 上存在最小值
上存在最小值![]() ,矛盾.
,矛盾.
利用归纳法和上面结论可得:对于任意![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
②其次证明当![]() 且
且![]() 时,
时,![]() ;当
;当![]() 且
且![]() 时,
时,![]() .
.
任取![]() ,设正整数
,设正整数![]() 满足
满足![]() ,则
,则![]() .
.
若存在![]() 使得
使得![]() ,则
,则![]() ,
,
即![]() .由于当
.由于当![]() 时,
时,![]() ,
,
所以![]() 在区间
在区间![]() ,
,![]() 有最小值
有最小值![]() ,矛盾.
,矛盾.
类似可证,当![]() 且
且![]() 时,
时,![]() .
.
③最后证明:当![]() 时,
时,![]() .
.
当![]() 时,
时,![]() 成立.当
成立.当![]() 时,由
时,由![]() 可知,
可知,
存在![]() 使得
使得![]() ,所以
,所以![]() .
.
当![]() 时,有:
时,有:![]()
若![]() ,则
,则![]() ,
,
所以![]() 在
在![]() ,
,![]() 上存在最小值,故不具有性质
上存在最小值,故不具有性质![]() ,故不成立.
,故不成立.
若![]() ,则
,则![]() ,
,![]() ,
,![]()
假设![]() ,则
,则![]() 在
在![]() ,
,![]() 上存在最小值,
上存在最小值,
故不具有性质![]() ,故假设不成立.
,故假设不成立.
所以当![]() 时,
时,![]() 对于任意
对于任意![]() 都成立.
都成立.
又![]() ,故当
,故当![]() 、
、![]() ,
,
所以![]() ,即
,即![]() .
.
所以当![]() 时,则存在正整数
时,则存在正整数![]() 使得
使得![]() ,则
,则![]()
所以当![]() 时,
时,![]() ,同理可证得当
,同理可证得当![]() 时,
时,![]() .
.
所以当![]() 时,必然存在正整数
时,必然存在正整数![]() ,使得
,使得![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() 显然成立;
显然成立;
所以综上所述:当![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
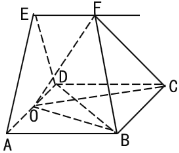
【题目】如图,![]() 是边长为2的正方形,平面
是边长为2的正方形,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作直线
作直线![]() ,
,![]() 是直线
是直线![]() 上一动点.
上一动点.
(1)求证:![]() ;
;
(2)若直线![]() 上存在唯一一点
上存在唯一一点![]() 使得直线
使得直线![]() 与平面
与平面![]() 垂直,求此时二面角
垂直,求此时二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,
,![]() ,若
,若![]() -
-![]()
![]() …,则称
…,则称![]() 是
是![]() 的“收缩数列”.其中,
的“收缩数列”.其中,![]() ,
,![]() 分别表示
分别表示![]() 中的最大数和最小数.已知
中的最大数和最小数.已知![]() 为无穷数列,其前
为无穷数列,其前![]() 项和为
项和为![]() ,数列
,数列![]() 是
是![]() 的“收缩数列”.
的“收缩数列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 项和;
项和;
(2)证明:![]() 的“收缩数列”仍是
的“收缩数列”仍是![]() ;
;
(3)若![]() ,求所有满足该条件的
,求所有满足该条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的2个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各取2个球.
(1)求取出的4个球中恰有1个红球的概率;
(2)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥A-BCD中,平面ABC丄平面ADC, AD丄AC,AD=AC, ![]() ,若此三棱锥的外接球表面积为
,若此三棱锥的外接球表面积为![]() ,则三棱锥A-BCD体积的最大值为( )
,则三棱锥A-BCD体积的最大值为( )
A.7B.12C.6D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在![]() 上的函数
上的函数![]() ,若函数
,若函数![]() 满足:
满足:
①在区间![]() 上单调递减,②存在常数p,使其值域为
上单调递减,②存在常数p,使其值域为![]() ,则称函数
,则称函数![]() 是函数
是函数![]() 的“逼进函数”.
的“逼进函数”.
(1)判断函数![]() 是不是函数
是不是函数![]() 的“逼进函数”;
的“逼进函数”;
(2)求证:函数![]() 不是函数
不是函数![]() ,的“逼进函数”
,的“逼进函数”
(3)若![]() 是函数
是函数![]() 的“逼进函数”,求a的值.
的“逼进函数”,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com