
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)根据椭圆的中点弦所在直线的斜率的性质,得到![]() ,得到
,得到![]() ,再结合椭圆所过的点的坐标满足椭圆方程,联立方程组,求得
,再结合椭圆所过的点的坐标满足椭圆方程,联立方程组,求得![]() ,进而求得椭圆的方程;
,进而求得椭圆的方程;
(Ⅱ)将直线方程与椭圆方程联立,消元,利用韦达定理得到两根和与两根积,将证明结果转化为证明直线![]() ,
,![]() 的斜率互为相反数,列式,可证.
的斜率互为相反数,列式,可证.
(Ⅰ)由题意,![]() ,
,
即![]() ① 又
① 又![]() ②
②
联立①①解得![]()
所以,椭圆![]() 的方程为:
的方程为:![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,由
,由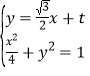 ,
,
得![]() ,
,
所以![]() ,即
,即![]() ,
,
又因为![]() ,所以,
,所以,![]() ,
,
![]() ,
,![]() ,
,
解法一:要证明![]() ,可转化为证明直线
,可转化为证明直线![]() ,
,![]() 的斜率互为相反数,只需证明
的斜率互为相反数,只需证明![]() ,即证明
,即证明![]() .
.
![]()
![]()
∴![]()
![]()
![]()
∴![]() ,∴
,∴![]() .
.
解法二:要证明![]() ,可转化为证明直线
,可转化为证明直线![]() ,
,![]() 与
与![]() 轴交点
轴交点![]() 、
、![]() 连线中点
连线中点![]() 的纵坐标为
的纵坐标为![]() ,即
,即![]() 垂直平分
垂直平分![]() 即可.
即可.
直线![]() 与
与![]() 的方程分别为:
的方程分别为:
![]() ,
,![]() ,
,
分别令![]() ,得
,得![]() ,
,![]()
而![]() ,同解法一,可得
,同解法一,可得![]()
![]() ,即
,即![]() 垂直平分
垂直平分![]() .
.
所以,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合A={x|ax2+2x+1=0,a∈R},
(1)若A只有一个元素,试求a的值,并求出这个元素;
(2)若A是空集,求a的取值范围;
(3)若A中至多有一个元素,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】—项“过关游戏”的规则规定:在第n关要抛一枚骰子n次,如果这n次抛掷所出现的点数之和大于![]() ,则算过关.那么,连过前3关的概率为_______.
,则算过关.那么,连过前3关的概率为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广州亚运会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向广州亚组委交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元.(
元.(![]() )
)
(1)写出该专营店一年内销售这种纪念章所获利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0(m∈R).
(1)判断直线l与圆C的位置关系;
(2)设直线l与圆C交于A,B两点,若直线l的倾斜角为120°,求弦AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据统计,某5家鲜花店今年4月的销售额和利润额资料如下表:
鲜花店名称 | A | B | C | D | E |
销售额x(千元) | 3 | 5 | 6 | 7 | 9 |
利润额y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法计算利润额y关于销售额x的回归直线方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鲜花店的销售额为8千元时,利用(1)的结论估计这家鲜花店的利润额是多少.
参考公式:回归方程![]() 中斜率和截距的最小二乘法估计值公式分别为
中斜率和截距的最小二乘法估计值公式分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com