
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
【答案】(1)![]() (y≠0);(2)
(y≠0);(2)![]()
【解析】
(1)设P(x,y)为轨迹Γ上任意一点,根据kPAkPB![]() ,得到
,得到![]() ,化简即得解;
,化简即得解;
(2)设MN:y=x+b,联立得到韦达定理,利用弦长公式表示弦长|MN|,O到直线MN的距离,继而表示△OMN的面积,利用导数研究单调性,求最值即可.
(1)设P(x,y)为轨迹Γ上任意一点,则根据kPAkPB![]() .
.
即![]() ,
,
整理得动点P的轨迹Γ的方程为:![]() (y≠0);
(y≠0);
(2)设MN:y=x+b,联立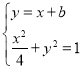 ,
,
整理得5x2+8bx+4b2﹣4=0,
△=5﹣b2>0,
设M(x1,y1),N(x2,y2),
则x1+x2![]() b,x1x2
b,x1x2![]() (b2﹣1),
(b2﹣1),
|MN|![]() |x1﹣x2|
|x1﹣x2|![]() ,
,
O到直线MN的距离d![]() ,
,
所以△OMN面积S![]() ,
,
设f(b)=5b2﹣b4,
则f′(b)=10b﹣4b3=0,
解得b=0或b=±![]() ,
,
又因为5﹣b2>0,
故b=0或b=±![]()
且S(0)=0,S(±![]() )
)![]() ,
,
故△OMN的面积S最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四面体ABCD中,平面DAC⊥底面ABC,![]() ,AD=CD=
,AD=CD=![]() ,O是AC的中点,E是BD的中点.
,O是AC的中点,E是BD的中点.
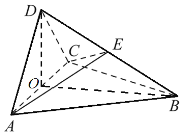
(1)证明:DO⊥底面ABC;
(2)求二面角D-AE-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cos ωx·sin![]() +a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π.
(1)求a和ω的值;
(2)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为鼓励人们绿色出行,乘坐地铁,地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策,不超过![]() 站的地铁票价如下表:
站的地铁票价如下表:
乘坐站数 |
|
|
|
票价(元) |
|
|
|
现有甲、乙两位乘客同时从起点乘坐同一辆地铁,已知他们乘坐地铁都不超过![]() 站.甲、乙乘坐不超过
站.甲、乙乘坐不超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() ;甲、乙乘坐超过
;甲、乙乘坐超过![]() 站的概率分别为
站的概率分别为![]() ,
, ![]() .
.
(1)求甲、乙两人付费相同的概率;
(2)设甲、乙两人所付费用之和为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,命题p:“x∈[1,2],x2﹣a≥0”,命题q:“x∈R,x2+2ax+2﹣a=0”.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax2+bx(e为自然对数的底,a,b为常数),曲线y=f(x)在x=0处的切线经过点A(﹣1,﹣1)
(1)求实数b的值;
(2)是否存在实数a,使得曲线y=f(x)所有切线的斜率都不小于2?若存在,求实数a的取值集合,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() ).
).
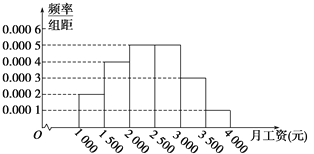
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
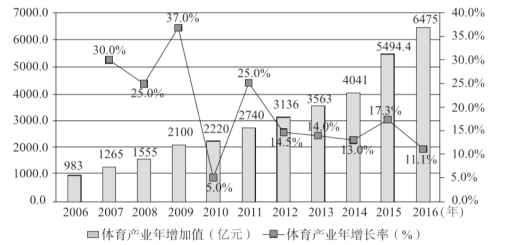
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com