
【题目】改革开放40年来,体育产业蓬勃发展反映了“健康中国”理念的普及.下图是我国2006年至2016年体育产业年增加值及年增速图.其中条形图表示体育产业年增加值(单位:亿元),折线图为体育产业年增长率(%).
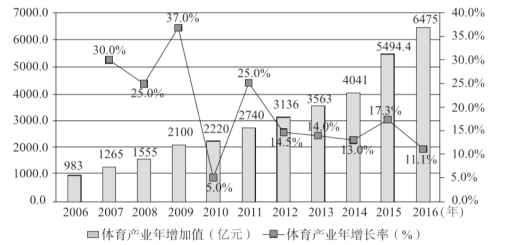
(Ⅰ)从2007年至2016年这十年中随机选出一年,求该年体育产业年增加值比前一年多![]() 亿元以上的概率;
亿元以上的概率;
(Ⅱ)从2007年至2011年这五年中随机选出两年,求至少有一年体育产业年增长率超过25%的概率;
(Ⅲ)由图判断,从哪年开始连续三年的体育产业年增长率方差最大?从哪年开始连续三年的体育产业年增加值方差最大?(结论不要求证明)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)从
;(Ⅲ)从![]() 年或
年或![]() 年开始连续三年的体育产业年增长率方差最大.从
年开始连续三年的体育产业年增长率方差最大.从![]() 年开始连续三年的体育产业年增加值方差最大.
年开始连续三年的体育产业年增加值方差最大.
【解析】
(Ⅰ)由图利用古典概型求值即可;(Ⅱ)求出任选两年的基本事件总数,列举满足条件的基本事件,即可求概率(Ⅲ)由题分析即可求解
(Ⅰ)设![]() 表示事件“从2007年至2016年这十年中随机选出一年,该年体育产业年增加值比前一年多
表示事件“从2007年至2016年这十年中随机选出一年,该年体育产业年增加值比前一年多![]() 亿元以上”.
亿元以上”.
根据题意,![]() .
.
(Ⅱ)从2007年至2011年这五年中有两年体育产业年增长率超过25%,设这两年为![]() ,
,![]() ,其它三年设为
,其它三年设为![]() ,
,![]() ,
,![]() ,从五年中随机选出两年,共有10种情况:
,从五年中随机选出两年,共有10种情况:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中至少有一年体育产业年增长率超过25%有7种情况,
,其中至少有一年体育产业年增长率超过25%有7种情况,
所以所求概率为![]() .
.
(Ⅲ)从![]() 年或
年或![]() 年开始连续三年的体育产业年增长率方差最大. 从
年开始连续三年的体育产业年增长率方差最大. 从![]() 年开始连续三年的体育产业年增加值方差最大.
年开始连续三年的体育产业年增加值方差最大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,A(﹣2,0),B(2,0),P为不在x轴上的动点,直线PA,PB的斜率满足kPAkPB![]() .
.
(1)求动点P的轨迹Γ的方程;
(2)若M,N是轨迹Γ上两点,kMN=1,求△OMN面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,在
上的奇函数,在![]() 上是增函数,且
上是增函数,且![]() ,给出下列结论,
,给出下列结论,
①若![]() 且
且![]() ,则
,则![]() ;
;
②若![]() 且
且![]() ,则
,则![]() ;
;
③若方程![]() 在
在![]() 内恰有四个不同的实根
内恰有四个不同的实根![]() ,
, ![]() ,
, ![]() ,
, ![]() ,则
,则![]() 或8;
或8;
④函数![]() 在
在![]() 内至少有5个零点,至多有13个零点.
内至少有5个零点,至多有13个零点.
其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
(1)若![]() ,则
,则![]() 恒成立;
恒成立;
(2)命题“若![]() ,则
,则![]() ”的逆否命题为“若
”的逆否命题为“若![]() ,则
,则![]() ”;
”;
(3)“命题![]() 为真”是“命题
为真”是“命题![]() 为真”的充分不必要条件;
为真”的充分不必要条件;
(4)命题“![]() ”的否定是“
”的否定是“![]() ”.
”.
其中正确的结论的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,PD//MA,MA⊥AD,PM⊥平面CDM,MA=AD![]() PD=1.
PD=1.
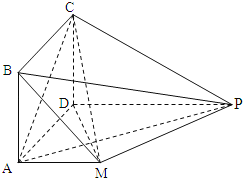
(1)求证:平面ABCD⊥平面AMPD;
(2)求三棱锥A﹣CMP的高.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com