
【题目】已知函数![]()
(1)讨论![]() 的极值;
的极值;
(2)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,
时,![]() 有极大值
有极大值![]() ,无极小值;(Ⅱ)
,无极小值;(Ⅱ)![]()
【解析】
【试题分析】(1)先对函数![]() ,
,![]() 求导,再分
求导,再分![]() 和
和![]() 两种情形讨论导函数值
两种情形讨论导函数值![]() (
(![]() )的符号,进而判定函数
)的符号,进而判定函数![]() 单调区间,求出函数
单调区间,求出函数![]() 的极值;(2)先将原不等式
的极值;(2)先将原不等式![]() 等价转化为
等价转化为![]() ,进而构造函数
,进而构造函数![]() (
(![]() ),将问题转化为求出
),将问题转化为求出![]() .然后借助题设条件先对函数
.然后借助题设条件先对函数![]() (
(![]() )求导,再对实数
)求导,再对实数![]() 分类运用导数的知识求出
分类运用导数的知识求出![]() =0,进而确定所求实数
=0,进而确定所求实数![]() 的取值范围。
的取值范围。
解:(Ⅰ)依题意![]() (
(![]() ),
),
①当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,无极值;
上单调递增,无极值;
②当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,无极小值.
,无极小值.
综上可知,当![]() 时,
时,![]() 无极值;当
无极值;当![]() 时,
时,![]() 有极大值
有极大值![]() ,无极小值.
,无极小值.
(Ⅱ)原不等式可化为![]()
![]() ,
,
记![]() (
(![]() ),只需
),只需![]() .
.
可得![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ,
,![]() 在
在![]() 上单调递增,所以当
上单调递增,所以当![]() 时,
时,![]() ,不合题意,舍去.
,不合题意,舍去.
(2)当![]() 时,
时,![]() ,
,
①当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递减.
上单调递减.
故当![]() 时,
时,![]() ,符合题意.
,符合题意.
②当![]() 时,记
时,记![]() (
(![]() ),
),
所以![]() ,
,![]() 在
在![]() 上单调递减.
上单调递减.
又![]() ,
,![]() ,
,
所以存在唯一![]() ,使得
,使得![]() .
.
当![]() 时,
时,![]() ,
,
从而![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,不符合要求,舍去.
,不符合要求,舍去.
综上可得,![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象与x轴交点为
的图象与x轴交点为![]() ,与此交点距离最小的最高点坐标为
,与此交点距离最小的最高点坐标为![]() .
.
(Ⅰ)求函数![]() 的表达式;
的表达式;
(Ⅱ)若函数![]() 满足方程
满足方程![]() ,求方程在
,求方程在![]() 内的所有实数根之和;
内的所有实数根之和;
(Ⅲ)把函数![]() 的图像的周期扩大为原来的两倍,然后向右平移
的图像的周期扩大为原来的两倍,然后向右平移![]() 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数![]() 的图像.若对任意的
的图像.若对任意的![]() ,方程
,方程![]() 在区间
在区间![]() 上至多有一个解,求正数k的取值范围.
上至多有一个解,求正数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述中正确的是( )
A. 若![]() ,则“
,则“![]() ”的充要条件是“
”的充要条件是“![]() ”
”
B. 函数![]() 的最大值是
的最大值是![]()
C. 命题“![]() ”的否定是“
”的否定是“![]() ”
”
D. ![]() 是一条直线,
是一条直线,![]() 是两个不同的平面,若
是两个不同的平面,若![]() 则
则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形公园![]() 中,
中,![]() ,
,![]() ,
,![]() ,公园的左下角阴影部分为以
,公园的左下角阴影部分为以![]() 为圆心,半径为
为圆心,半径为![]() 的
的![]() 圆面的人工湖,现设计修建一条与圆相切的观光道路
圆面的人工湖,现设计修建一条与圆相切的观光道路![]() (点
(点![]() 分别在
分别在![]() 与
与![]() 上),
上),![]() 为切点,设
为切点,设![]() .
.

(1)试求观光道路![]() 长度的最大值;
长度的最大值;
(2)公园计划在道路![]() 的右侧种植草坪,试求草坪
的右侧种植草坪,试求草坪![]() 的面积最大值.
的面积最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样的方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
附:![]() 的观测值
的观测值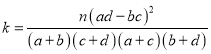
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
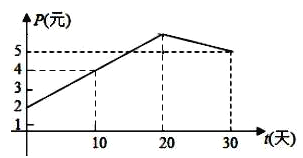
【题目】某上市股票在30天内每股的交易价格P(元)与时间t(天)组成有序数对![]() ,点
,点![]() 落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
落在如图所示的两条线段上.该股票在30天内(包括30天)的日交易量M(万股)与时间t(天)的部分数据如下表所示:
第t天 | 6 | 13 | 20 | 27 |
M(万股) | 34 | 27 | 20 | 13 |
(1)根据提供的图象,写出该股票每股交易价格P(元)与时间t(天)所满足的函数关系式![]() ______;
______;
(2)根据表中数据,写出日交易量M(万股)与时间t(天)的一次函数关系式:![]() ______;
______;
(3)用y(万元)表示该股票日交易额,写出y关于t的函数关系式,并求在这30天内第几天日交易额最大,最大值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com