练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，设向量， ，其中为的两个内角.

    （1）若，求证： 为直角；

    （2）若，求证： 为锐角.

    【答案】（1）见解析（2）见解析

    【解析】试题分析：（1）借助平面向量的坐标形式的数量积公式建立方程，然后运用诱导公式分析推证；（2）借助平面向量的坐标形式的数量积公式建立方程，即，也即然后运用两角和的正切公式分析推证，即：

    （1）易得，

    因为，所以，即.

    因为，且函数在内是单调减函数，

    所以，即为直角.

    （2）因为，所以，

    即.

    因为是三角形内角，所以，

    于是，因而中恰有一个是钝角，∴，

    从而，

    所以，即证为锐角

    注：（2）解得后，得与异号，

    若，

    则

    于是，在中，有两个钝角和，这与三角形内角和定理矛盾，不可能

    于是必有，即证为锐角

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】定义在R上的函数f（x）满足：①f（0）=0，②f（x）+f（1﹣x）=1，③f（ ）= f（x）且当0≤x1＜x2≤1时，f（x1）≤f（x2），则f（ ）+f（ ）等于（ ）
    A.1
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，菱形ABCD与正三角形BCE的边长均为2，它们所在平面互相垂直，FD⊥平面ABCD，且 ．

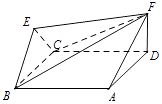
    （1）若∠BCD=60°，求证：BC⊥EF；
    （2）若∠CBA=60°，求直线AF与平面FBE所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知抛物线C：y2=4x，过焦点F斜率大于零的直线l交抛物线于A、B两点，且与其准线交于点D．
    （Ⅰ）若线段AB的长为5，求直线l的方程；
    （Ⅱ）在C上是否存在点M，使得对任意直线l，直线MA，MD，MB的斜率始终成等差数列，若存在求点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中， 是自然对数的底数.

    （1）当时，求曲线在处的切线方程；

    （2）求函数的单调减区间；

    （3）若在恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列的前项和为，且.

    （1）求证：数列为等比数列；

    （2）设数列的前项和为，求证： 为定值；

    （3）判断数列中是否存在三项成等差数列，并证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列命题中

    ① 非零向量满足，则的夹角为；

    ②

    ＞0是的夹角为锐角的充要条件；

    ③若则必定是直角三角形；

    ④△ABC的外接圆的圆心为O，半径为1，若,且，则向量在向量方向上的投影为.

    以上命题正确的是 __________ （注：把你认为正确的命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

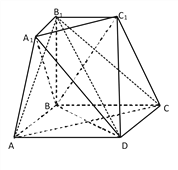
    【题目】如图所示的几何体是由棱台 和棱锥拼接而成的组合体，其底面四边形是边长为 的菱形，且 ， 平面 ， ．

    （1）求证：平面 平面 ；

    （2）求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，（其中， 为自然对数的底数， ……）.

    （1）令，求的单调区间；

    （2）已知在处取得极小值，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案