
【题目】如图,已知抛物线C:y2=4x,过焦点F斜率大于零的直线l交抛物线于A、B两点,且与其准线交于点D.
(Ⅰ)若线段AB的长为5,求直线l的方程;
(Ⅱ)在C上是否存在点M,使得对任意直线l,直线MA,MD,MB的斜率始终成等差数列,若存在求点M的坐标;若不存在,请说明理由.
【答案】解:(Ⅰ)焦点F(1,0)
∵直线l的斜率不为0,所以设l:x=my+1,
A(x1 , y1),B(x2 , y2)
由 ![]() 得y2﹣4my﹣4=0,
得y2﹣4my﹣4=0,
y1+y2=4m,y1y2=﹣4,![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∴直线l的斜率k2=4,
∵k>0,∴k=2,
∴直线l的方程为2x﹣y﹣2=0.
(Ⅱ)设M(a2 , 2a),
kMA= ![]() =
= ![]() ,
,
同理,kMB= ![]() ,kMD=
,kMD=  ,
,
∵直线MA,MD,MB的斜率始终成等差数列,
∴2  =
= ![]() +
+ ![]() 恒成立;
恒成立;
∴ ![]() =
= ![]() ,
,
又∵y1+y2=4m,y1y2=﹣4,
∴(a2﹣1)(m+ ![]() )=0,
)=0,
∴a=±1,
∴存在点M(1,2)或M(1,﹣2),使得对任意直线l,
直线MA,MD,MB的斜率始终成等差数列.
【解析】(Ⅰ)设l:x=my+1,A(x1 , y1),B(x2 , y2),则联立方程化简可得y2﹣4my﹣4=0,从而可得 ![]() ,从而求直线l的方程;
,从而求直线l的方程;
(Ⅱ)设M(a2 , 2a),则kMA= ![]() =
= ![]() ,kMB=
,kMB= ![]() ,kMD=
,kMD= ![]() ,则
,则 ![]() =
= ![]() ,从而可得(a2﹣1)(m+
,从而可得(a2﹣1)(m+ ![]() )=0,从而求出点M的坐标.
)=0,从而求出点M的坐标.
【考点精析】利用一般式方程对题目进行判断即可得到答案,需要熟知直线的一般式方程:关于![]() 的二元一次方程
的二元一次方程![]() (A,B不同时为0).
(A,B不同时为0).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,首项a1=1,公比q>0,其前n项和为Sn,且S1+a1,S3+a3,S2+a2成等差数列.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足![]() ,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
,Tn为数列{bn}的前n项和,若Tn≥m恒成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的前n项和为Sn , 对任意n∈N* , 点(an , Sn)都在函数 ![]() 的图象上.
的图象上.
(1)求数列{an}的首项a1和通项公式an;
(2)若数列{bn}满足 ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)已知数列{cn}满足 ![]() .若对任意n∈N* , 存在
.若对任意n∈N* , 存在 ![]() ,使得c1+c2+…+cn≤f(x)﹣a成立,求实数a的取值范围.
,使得c1+c2+…+cn≤f(x)﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
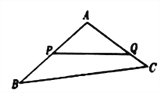
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x∈A,且A={x|a﹣1<x<a+1},命题q:x∈B,且B={x|x2﹣4x+3≥0}
(Ⅰ)若A∩B=,A∪B=R,求实数a的值;
(Ⅱ)若p是q的充分条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
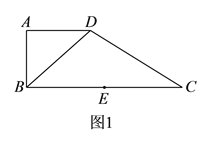
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
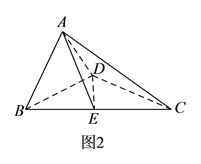
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com