
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)已知![]() 在
在![]() 处取得极小值,求实数
处取得极小值,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)求导函数的导数得![]() ,再根据是否变号进行分类讨论单调性:当
,再根据是否变号进行分类讨论单调性:当![]() 时,导函数不变号,为单调递增;当
时,导函数不变号,为单调递增;当![]() 时,导函数先负后正,对应单调区间为先减后增(2)由题意得
时,导函数先负后正,对应单调区间为先减后增(2)由题意得![]() ,结合(1)根据导函数
,结合(1)根据导函数![]() 单调性分类讨论在
单调性分类讨论在![]() 处是否为极小值:当
处是否为极小值:当![]() 时,
时, ![]() 在
在![]() 附近先减后增,为极小值;当
附近先减后增,为极小值;当![]() 时,按
时,按![]() 与零大小关系进行二次讨论:
与零大小关系进行二次讨论: ![]() ,
, ![]() 单调递增;
单调递增; ![]() 在
在![]() 附近先减后增,为极小值;当
附近先减后增,为极小值;当![]() 时,
时, ![]() ,无极值;
,无极值; ![]() 时,
时, ![]() 单调递减;
单调递减; ![]() 在
在![]() 附近先增后减,为极大值;综上可得实数
附近先增后减,为极大值;综上可得实数![]() 的取值范围.
的取值范围.
试题解析:解: (Ⅰ) 因为![]() ,
,
所以![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 的单调递增区间为
的单调递增区间为![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]()
综上可得,当![]() 时,
时, ![]() 在
在![]() 上单调递增
上单调递增
当![]() 时,
时, ![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(Ⅱ)由题意得![]() ,
, ![]() ,
,
(1)当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 处取得极小值,符合题意.
处取得极小值,符合题意.
(2)当![]() 时,
时, ![]() , 由(Ⅰ)知
, 由(Ⅰ)知![]() 在
在![]() 单调递增,
单调递增,
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 处取得极小值,符合题意.
处取得极小值,符合题意.
(3)当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在区间
在区间![]() 单调递减,
单调递减, ![]() 在区间
在区间![]() 单调递增,
单调递增,
所以![]() 在
在![]() 处取得最小值,即
处取得最小值,即![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在
在![]() 处无极值,不符合题意.
处无极值,不符合题意.
(4)当![]() 时,
时, ![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 的减区间为
的减区间为![]() ,
,
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以![]() 在
在![]() 处取得极大值,不符合题意,
处取得极大值,不符合题意,
综上可知,实数![]() 的取值范围为
的取值范围为![]() .
.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
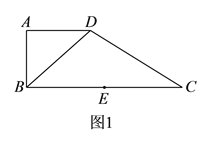
【题目】如图![]() ,在直角梯形
,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,连接
,连接![]() ,
, ![]() ,
, ![]() ,得到如图
,得到如图![]() 所示的几何体.
所示的几何体.
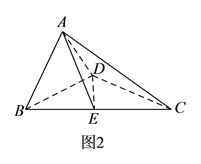
(Ⅰ)求证: ![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,
, ![]() 与其在平面
与其在平面![]() 内的正投影所成角的正切值为
内的正投影所成角的正切值为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面四边形ABCD中,AD=1,CD=2,AC= ![]() .
. 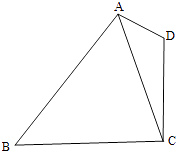
(1)求cos∠CAD的值;
(2)若cos∠BAD=﹣ ![]() ,sin∠CBA=
,sin∠CBA= ![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A、B、C,田忌的三匹马分别为a、b、c.三匹马各比赛一次,胜两场者为获胜.若这六匹马比赛的优劣程度可以用以下不等式表示:A>a>B>b>C>c. (Ⅰ)如果双方均不知道对方马的出场顺序,求田忌获胜的概率;
(Ⅱ)为了得到更大的获胜概率,田忌预先派出探子到齐王处打探实情,得知齐王第一场必出上等马.那么,田忌应怎样安排出马的顺序,才能使自己获胜的概率最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=7,a5+a7=26,数列{an}的前n项和为Sn .
(Ⅰ)求an;
(Ⅱ)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线的方程为x﹣2y﹣5=0.
(1)求直线BC的方程;
(2)求直线BC关于CM的对称直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱ABC﹣A1B1C1的所有棱长均为a,M是BC的中点,侧面B1C1CB⊥底面ABC,且AC1⊥BC.
(Ⅰ)求证:BC⊥C1M;
(Ⅱ)求二面角A1﹣AB﹣C的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com