
 ,P是椭圆C在第一象限内的一点,且|PF1|-|PF2|=1.
,P是椭圆C在第一象限内的一点,且|PF1|-|PF2|=1. 解:(1)依题可设椭圆方程为
解:(1)依题可设椭圆方程为
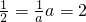 ,b2=a2-12=3-------------(2分)
,b2=a2-12=3-------------(2分) .-------------------(3分)
.-------------------(3分) -------(2分)
-------(2分) 得
得 或
或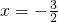 (舍去)
(舍去) -------------------(4分)
-------------------(4分)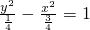 -------------------(2分)
-------------------(2分) 得
得 ------------------(3分)
------------------(3分)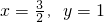 ∴
∴ -------------------(4分)
-------------------(4分) -------------------(1分)
-------------------(1分) ,得s=0-------------------(2分)
,得s=0-------------------(2分) ,∴t=±2-------------------(3分)
,∴t=±2-------------------(3分) ,∴
,∴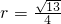 ,
,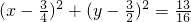 -------------(6分)
-------------(6分)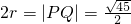 ,∴
,∴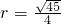 ,∴圆G为:
,∴圆G为: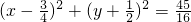 ------------(7分)
------------(7分)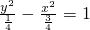 的上支,从而可得P为椭圆与双曲线的交点,联立
的上支,从而可得P为椭圆与双曲线的交点,联立 ,
,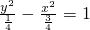 可求
可求 可求Q
可求Q 或
或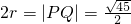 ,,从而可得圆的方程
,,从而可得圆的方程

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| AF2 |
| F2B |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2011年广东省汕头市高三质量测评数学试卷2(理科)(解析版) 题型:解答题
 ,P是椭圆C在第一象限内的一点,且|PF1|-|PF2|=1.
,P是椭圆C在第一象限内的一点,且|PF1|-|PF2|=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com