
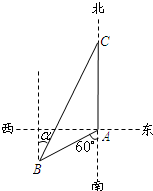
 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.| BC |
| 2 |
| AB |
| sinα |
| BC |
| sin120° |
| ABsin120° |
| BC |
12×
| ||||
| 28 |
3
| ||
| 14 |
3
| ||
| 14 |
| AC2+BC2-AB2 |
| 2AC×BC |
| 202+282-122 |
| 2×20×28 |
| 13 |
| 14 |
| 1-cos2α |
1-(
|
3
| ||
| 14 |
3
| ||
| 14 |


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
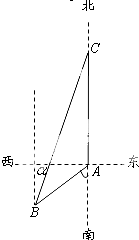 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.则sinα=
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.则sinα=3
| ||
| 14 |
3
| ||
| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
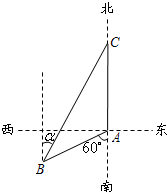 如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.则渔船甲的速度为
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上.则渔船甲的速度为3
| ||
| 14 |
3
| ||
| 14 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省泉州四校高三第二次联考考试理科数学 题型:解答题
.(本小题满分13分)如图,渔船甲位于岛屿 的南偏西
的南偏西 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东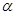 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求 的值.
的值.

查看答案和解析>>
科目:高中数学 来源:2013届广东省高二上学期期末考试理科数学 题型:填空题
如图,渔船甲位于岛屿 的南偏西
的南偏西 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.则渔船甲的速度为
海里/小时,
的方向追赶渔船乙,刚好用2小时追上.则渔船甲的速度为
海里/小时, 。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com