
【题目】已知函数f(x)![]() x2+ax+lnx(a∈R)
x2+ax+lnx(a∈R)
(1)讨论函数f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2且|x1﹣x2|![]() ,求|f(x1)﹣f(x2)|的最大值.
,求|f(x1)﹣f(x2)|的最大值.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)求导可得![]() ,再分
,再分![]() ,
,![]() 讨论
讨论![]() 与0的大小关系,进而得出单调性情况;
与0的大小关系,进而得出单调性情况;
(2)表示出![]() ,构造函数
,构造函数![]() ,利用导数求其最大值即可.
,利用导数求其最大值即可.
(1)![]() ,设μ(x)=x2+ax+1,则μ(0)=1>0,对称轴为
,设μ(x)=x2+ax+1,则μ(0)=1>0,对称轴为![]() ,
,
①当![]() ,即a≥0时,在(0,+∞)上,
,即a≥0时,在(0,+∞)上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
②当![]() ,即a<0时,
,即a<0时,![]() =a2﹣4=0得a=±2,
=a2﹣4=0得a=±2,
(i)当﹣2≤a<0时,在(0,+∞)上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
(ii)当a<﹣2时,令![]() =0得
=0得![]() ,
,
在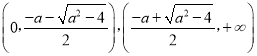 上,
上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
在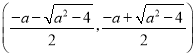 上,
上,![]() <0,f(x)是减函数;
<0,f(x)是减函数;
(2)由(1)知,f(x)得两个极值点x1,x2满足x2+ax+1=0,故x1+x2=﹣a,x1x2=1,
不妨设0<x1<1<x2,则f(x)在(x1,x2)上是减函数,
∴![]() ,
,
令![]() ,设函数
,设函数![]() ,则
,则![]() ,
,
∴h(t)在(1,+∞)上为增函数,
由![]() ,则
,则![]() ,解得1<x2≤2,故
,解得1<x2≤2,故![]() ,
,
∴![]() ,
,
∴|f(x1)﹣f(x2)|的最大值为![]() .
.


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,平面
,平面![]() 平面PAD,E是
平面PAD,E是![]() 的中点,F是DC上一点,G是PC上一点,且
的中点,F是DC上一点,G是PC上一点,且![]() ,
,![]() .
.
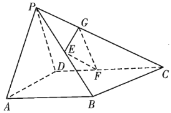
(1)求证:平面![]() 平面PAB;
平面PAB;
(2)若![]() ,
,![]() ,求直线PB与平面ABCD所成角的正弦值.
,求直线PB与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某项针对我国《义务教育数学课程标准》的研究中,列出各个学段每个主题所包含的条目数(如下表),下图是统计表的条目数转化为百分比,按各学段绘制的等高条形图,由图表分析得出以下四个结论,其中错误的是( )
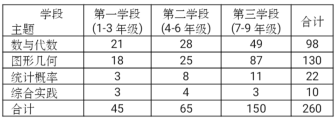
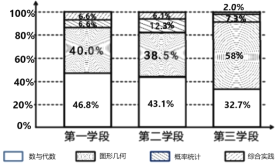
A.除了“综合实践”外,其它三个领域的条目数都随着学段的升高而增加,尤其“图象几何” 在第三学段增加较多,约是第二学段的![]() 倍.
倍.
B.所有主题中,三个学段的总和“图形几何”条目数最多,占50%,综合实践最少,约占4% .
C.第一、二学段“数与代数”条目数最多,第三学段“图形几何”条目数最多.
D.“数与代数”条目数虽然随着学段的增长而增长,而其百分比却一直在减少.“图形几何”条目数,百分比都随学段的增长而增长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某初中学校学生睡眠状况,在该校全体学生中随机抽取了容量为120的样本,统计睡眠时间(单位:![]() ).经统计,时间均在区间
).经统计,时间均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图:
分成6组,制成如图所示的频率分布直方图:

(1)世界卫生组织表明,该年龄段的学生睡眠时间![]() 服从正态分布
服从正态分布![]() ,其标准为:该年龄段的学生睡眠时间的平均值
,其标准为:该年龄段的学生睡眠时间的平均值![]() ,方差
,方差![]() .根据
.根据![]() 原则,用样本估计总体,判断该初中学校学生睡眠时间在区间
原则,用样本估计总体,判断该初中学校学生睡眠时间在区间![]() 上是否达标?
上是否达标?
(参考公式:![]() ,
,![]() ,
,![]() )
)
(2)若规定睡眠时间不低于![]() 为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下
为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下![]() 列联表所示:
列联表所示:
优质睡眠 | 非优质睡眠 | 合计 | |
男 | 60 | ||
女 | 19 | ||
合计 |
将列联表数据补充完整,并判断是否有![]() 的把握认为优质睡眠与性别有关系,并说明理由;
的把握认为优质睡眠与性别有关系,并说明理由;
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: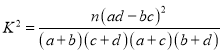 ,其中
,其中![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l:x﹣ty+1=0(t>0)和抛物线C:y2=4x相交于不同两点A、B,设AB的中点为M,抛物线C的焦点为F,以MF为直径的圆与直线l相交另一点为N,且满足|MN|![]() |NF|,则直线l的方程为_____.
|NF|,则直线l的方程为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点P(2,1),且离心率为
经过点P(2,1),且离心率为![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设O为坐标原点,在椭圆短轴上有两点M,N满足![]() ,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
,直线PM、PN分别交椭圆于A,B.探求直线AB是否过定点,如果经过定点请求出定点的坐标,如果不经过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 的参数方程为
的参数方程为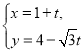 (
(![]() 是参数),以原点为极点,
是参数),以原点为极点,![]() 轴的非负半轴
轴的非负半轴
为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() 在曲线
在曲线![]() 上,曲线
上,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求点
垂直,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某果园今年的脐橙丰收了,果园准备利用互联网销售.为了更好的销售,现随机摘下了![]() 个脐橙进行测重,其质量分布在区间
个脐橙进行测重,其质量分布在区间![]() 内(单位:克),统计质量的数据作出频率分布直方图如下图所示:
内(单位:克),统计质量的数据作出频率分布直方图如下图所示:
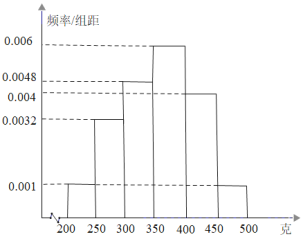
(1)按分层抽样的方法从质量落在![]() ,
,![]() 的脐橙中随机抽取
的脐橙中随机抽取![]() 个,再从这
个,再从这![]() 个脐橙中随机抽
个脐橙中随机抽![]() 个,求这
个,求这![]() 个脐橙质量都不小于
个脐橙质量都不小于![]() 克的概率;
克的概率;
(2)以各组数据的中间数值代表这组数据的平均水平,以频率代表概率,已知该果园的脐橙树上大约还有![]() 个脐橙待出售,某电商提出两种收购方案:甲:所有脐橙均以
个脐橙待出售,某电商提出两种收购方案:甲:所有脐橙均以![]() 元/千克收购;乙:低于
元/千克收购;乙:低于![]() 克的脐橙以
克的脐橙以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.请通过计算为该果园选择收益最好的方案.
元/个收购.请通过计算为该果园选择收益最好的方案.
(参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com