
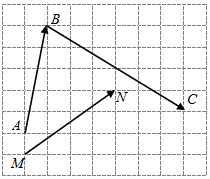
 向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2.
向量$\overrightarrow{AB}$,$\overrightarrow{BC}$,$\overrightarrow{MN}$在正方形网格中的位置如图所示,若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$(λ,μ∈R),则$\frac{λ}{μ}$=2. 分析 可在图中作出向量$\overrightarrow{i},\overrightarrow{j}$,根据图形便可得出$\overrightarrow{AB}=\overrightarrow{i}+5\overrightarrow{j},\overrightarrow{BC}=6\overrightarrow{i}-4\overrightarrow{j}$,$\overrightarrow{MN}=4\overrightarrow{i}+3\overrightarrow{j}$,根据$\overrightarrow{MN}=λ\overrightarrow{AB}+μ\overrightarrow{BC}$进行向量的数乘运算便可得出$\overrightarrow{MN}=(λ+6μ)\overrightarrow{i}+(5λ-4μ)\overrightarrow{j}$,这样根据平面向量基本定理即可得出关于λ,μ的二元一次方程组,解出λ,μ,从而便可求出$\frac{λ}{μ}$的值.
解答  解:如图,作向量$\overrightarrow{i},\overrightarrow{j}$,则:
解:如图,作向量$\overrightarrow{i},\overrightarrow{j}$,则:
$\overrightarrow{AB}=\overrightarrow{i}+5\overrightarrow{j},\overrightarrow{BC}=6\overrightarrow{i}-4\overrightarrow{j}$,$\overrightarrow{MN}=4\overrightarrow{i}+3\overrightarrow{j}$;
∴$\overrightarrow{MN}=λ\overrightarrow{AB}+μ\overrightarrow{BC}$=$λ(\overrightarrow{i}+5\overrightarrow{j})+μ(6\overrightarrow{i}-4\overrightarrow{j})$=$(λ+6μ)\overrightarrow{i}+(5λ-4μ)\overrightarrow{j}$;
∴根据平面向量基本定理得,$\left\{\begin{array}{l}{λ+6μ=4}\\{5λ-4μ=3}\end{array}\right.$;
解得$\left\{\begin{array}{l}{λ=1}\\{μ=\frac{1}{2}}\end{array}\right.$;
∴$\frac{λ}{μ}=2$.
故答案为:2.
点评 考查向量加法的平行四边形法则,向量数乘的几何意义,以及向量的数乘运算,平面向量基本定理.


科目:高中数学 来源: 题型:解答题
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 5 | 10 | 15 | 47 | x |
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 人数 | 2 | 3 | 10 | y | 2 |
| 女士 | 男士 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 吉林市某中学利用周末组织教职员工进行了一次冬季户外健身活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.
吉林市某中学利用周末组织教职员工进行了一次冬季户外健身活动,有N人参加,现将所有参加人员按年龄情况分为[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55)等七组,其频率分布直方图如图所示.已知[35,40)之间的参加者有8人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有一个 | B. | 两个 | C. | 有三个 | D. | 四个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com